题目内容
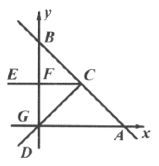
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点B,点C是AB的中点,∠ECD绕点C按顺时针旋转,且∠ECD=45°,∠ECD的一边CE交y轴于点F,开始时另一边CD经过点O,点G坐标为(-2,0),当∠ECD旋转过程中,射线CD与x轴的交点由点O到点G的过程中,则经过点B、C、F三点的圆的圆心所经过的路径长为( )
与x轴交于点A,与y轴交于点B,点C是AB的中点,∠ECD绕点C按顺时针旋转,且∠ECD=45°,∠ECD的一边CE交y轴于点F,开始时另一边CD经过点O,点G坐标为(-2,0),当∠ECD旋转过程中,射线CD与x轴的交点由点O到点G的过程中,则经过点B、C、F三点的圆的圆心所经过的路径长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
先确定点B、A、C的坐标,①当点G在点O时,点F的坐标为(0,2),此时点F、B、C三点的圆心为BC的中点,坐标为(1,3);②当直线OD过点G时,利用相似求出点F的坐标,根据圆心在弦的垂直平分线上确定圆心在线段BC的垂直平分线上,故纵坐标为![]() ,利用两点间的距离公式求得圆心的坐标,由此可求圆心所走的路径的长度.
,利用两点间的距离公式求得圆心的坐标,由此可求圆心所走的路径的长度.
∵直线![]() 与x轴交于点A,与y轴交于点B,
与x轴交于点A,与y轴交于点B,
∴B(0,4),A(4,0),
∵点C是AB的中点,
∴C(2,2),
①当点G在点O时,点F的坐标为(0,2),此时点F、B、C三点的圆心为BC的中点,坐标为(1,3);
②当直线OD过点G时,如图,
连接CN,OC,则CN=ON=2,∴OC=![]() ,
,
∵G(-2,0),
∴直线GC的解析式为:![]() ,∴直线GC与y轴交点M(0,1),
,∴直线GC与y轴交点M(0,1),
过点M作MH⊥OC,∵∠MOH=45![]() ,∴MH=OH=
,∴MH=OH=![]() ,
,
∴CH=OC-OH=![]() ,
,
∵∠NCO=∠FCG=45![]() ,∴∠FCN=∠MCH,
,∴∠FCN=∠MCH,
又∵∠FNC=∠MHC,
∴△FNC∽△MHC,
∴![]() ,即
,即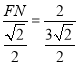 ,得FN=
,得FN=![]() ,∴F(
,∴F(![]() ,0),
,0),
此时过点F、B、C三点的圆心在BF的垂直平分线上,设圆心坐标为(x,![]() ),
),
则![]() ,解得
,解得![]() ,
,
当∠ECD旋转过程中,射线CD与x轴的交点由点O到点G的过程中,则经过点B、C、F三点的圆的圆心所经过的路径为线段,即由BC的中点到点(![]() ,
,![]() ),
),
∴所经过的路径长=![]() .
.
故选:A.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案【题目】在一个不透明的布袋中,有三个除颜色外其它均相同的小球,其中两个黑色,一个红色.
(1)请用表格或树状图求出:一次随机取出2个小球,颜色不同的概率.
(2)如果老师在布袋中加入若干个红色小球.然后小明通过做实验的方式猜测加入的小球数,小 明每次換出一个小球记录下慎色并放回,实验数据如下表:
实验次数 | 100 | 200 | 300 | 400 | 500 | 1000 |
摸出红球 | 78 | 147 | 228 | 304 | 373 | 752 |
请你帮小明算出老师放入了多少个红色小球.
【题目】学校为了解九年级学生对“八礼四仪”的掌握情况,对该年级的500名同学进行问卷测试,并随机抽取了10名同学的问卷,统计成绩如下:
得分 | 10 | 9 | 8 | 7 | 6 |
人数 | 3 | 3 | 2 | 1 | 1 |
(1)计算这10名同学这次测试的平均得分;
(2)如果得分不少于9分的定义为“优秀”,估计这 500名学生对“八礼四仪”掌握情况优秀的人数;
(3)小明所在班级共有40人,他们全部参加了这次测试,平均分为7.8分.小明的测试成绩是8分,小明说,我的测试成绩在班级中等偏上,你同意他的观点吗?为什么?