题目内容
14、在平面内用12根火柴棒首尾顺次相接搭成三角形,能搭成
1
个直角三角形,搭成2
个等腰三角形.分析:根据三角形的三边关系:在三角形中,任何两边和大于第三边,任何两边差小于第三边;则三角形的一边不能为1,也不能为6;即三边分别为2、3、4、5,据此即可判断直角三角形的以及等腰三角形的个数.
解答:解:∵在三角形中,任何两边和大于第三边,任何两边差小于第三边,
∴三角形的一边不能为1,也不能为6;
当一边为2时,则另两边为5,5;
当一边为3时,则另两边为4,5;
当一边为4时,则另两边为4,4;
所以,直角三角形个数为1,等腰三角形个数为2个.
∴三角形的一边不能为1,也不能为6;
当一边为2时,则另两边为5,5;
当一边为3时,则另两边为4,5;
当一边为4时,则另两边为4,4;
所以,直角三角形个数为1,等腰三角形个数为2个.
点评:本题考查了三角形三边的关系,即在三角形中,任何两边和大于第三边,任何两边差小于第三边.

练习册系列答案
相关题目
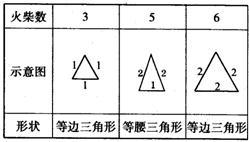
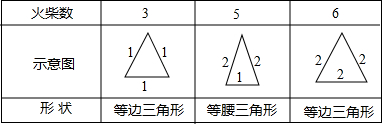 如图,在平面内,分别用3根、5根、6根火柴首尾顺次相接,能搭成一个不同形状的三角形.
如图,在平面内,分别用3根、5根、6根火柴首尾顺次相接,能搭成一个不同形状的三角形.