题目内容
CD是Rt△ABC斜边上的高线,AD、BD是方程x2-6x+4=0的两根,则△ABC的面积为分析:由AD、BD是方程x2-6x+4=0的两根可以得到AD+BD=6,AD•BD=4,易证△DBC∽△DCA,可得到CD=
=2,而△ABC的面积=
×(AD+BD)×CD,由此可以求出面积.
| AD×BD |
| 1 |
| 2 |
解答:解:∵AD、BD是方程x2-6x+4=0的两根,
∴AD+BD=6,AD•BD=4,
∵∠ACB=90°,CD⊥AB于D,
∴△DBC∽△DCA,
∴
=
,
∴CD2=AD•BD,
∴CD=
=2,
∴S△ABC=
×(AD+BD)×CD=6.
故填:6.
∴AD+BD=6,AD•BD=4,
∵∠ACB=90°,CD⊥AB于D,
∴△DBC∽△DCA,
∴
| CD |
| AD |
| DB |
| CD |
∴CD2=AD•BD,
∴CD=
| AD×BD |
∴S△ABC=
| 1 |
| 2 |
故填:6.
点评:此题难点是利用相似求得斜边上的高,解题关键是得到所求三角形相应的底与高的长.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
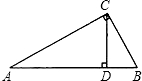 如图,CD是Rt△ABC斜边上的高,AC=4,BC=3,则cos∠BCD的值是( )
如图,CD是Rt△ABC斜边上的高,AC=4,BC=3,则cos∠BCD的值是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =( )
=( )




 =( )
=( )
 B.
B.
 D.
D.
 如图,CD是Rt△ABC斜边AB边上的高,AB=10cm,BC=8cm,则sin∠ACD=
如图,CD是Rt△ABC斜边AB边上的高,AB=10cm,BC=8cm,则sin∠ACD=



