题目内容
（2010•市南区模拟）（1）化简：
+
；
（2）解不等式组：
．
| 1 |
| a+1 |
| 1 |
| a(a+1) |
（2）解不等式组：
|
分析：（1）先通分，再根据同分母分式加减法法则：同分母的分式想加减，分母不变，把分子相加减，即可得出答案．
（2）首先解不等式组中的每个不等式，然后确定两个不等式的解集的公共部分，即可确定不等式组的解集．
（2）首先解不等式组中的每个不等式，然后确定两个不等式的解集的公共部分，即可确定不等式组的解集．
解答：解：（1）
+
=
+
=
=
；
（2）
，
由①得：x≤3，
由②得：x＞-2，
故不等式组的解集是-2＜x≤3．
| 1 |
| a+1 |
| 1 |
| a(a+1) |
=
| a |
| a(a+1) |
| 1 |
| a(a+1) |
=
| a+1 |
| a(a+1) |
=
| 1 |
| a |
（2）
|
由①得：x≤3，
由②得：x＞-2，
故不等式组的解集是-2＜x≤3．
点评：（1）主要考查了分式的加减法运算，通分是解题关键．
（2）考查了解一元一次不等式组，把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．
（2）考查了解一元一次不等式组，把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．
练习册系列答案
阅读快车系列答案
相关题目
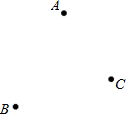（2010•市南区模拟）上海世博会要修建一处公共设施，使它到三个场馆A、B、C的距离相等，三个场馆A、B、C的位置如图所示，请你在图中确定这处公共设施（用点P表示）的位置．