题目内容
如图,AB∥CD,学习兴趣小组分别探讨下面三个图形,∠APC与∠PAB、∠PCD的关系,请你从所得的关系中任意选两个加以说明(适当添加辅助线,其实并不难)。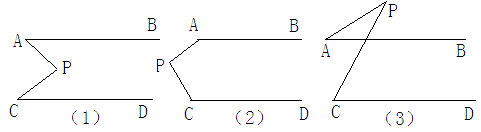

过P作PM∥AB (3分)
∵AB∥CD∥PM
如图①
∴∠PAB=∠APM
∴∠PCD=∠CPM (4分) ∠APC=∠PAB+∠PCD (6分)
如图②
∵AB∥CD∥PM ∠PAB+∠APM=180° ∠PCD+∠CPM=180° (4分)
∴∠PAB+∠PCD+∠APC=360° (6分)
如图③
∵AB∥CD∥P N ∴∠PCD=∠PMB 又∵∠PMB为△PAM外角
∴∠APC=∠PCD-∠PAB
∴∠APC=360°-(∠PAB+∠PCD)
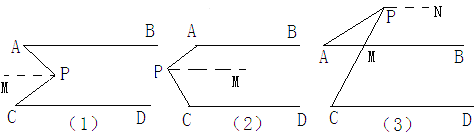
∵AB∥CD∥PM
如图①
∴∠PAB=∠APM
∴∠PCD=∠CPM (4分) ∠APC=∠PAB+∠PCD (6分)
如图②
∵AB∥CD∥PM ∠PAB+∠APM=180° ∠PCD+∠CPM=180° (4分)
∴∠PAB+∠PCD+∠APC=360° (6分)
如图③
∵AB∥CD∥P N ∴∠PCD=∠PMB 又∵∠PMB为△PAM外角
∴∠APC=∠PCD-∠PAB
∴∠APC=360°-(∠PAB+∠PCD)

关键过转折点作出平行线,根据两直线平行,内错角相等,或结合三角形的外角性质求证即可.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
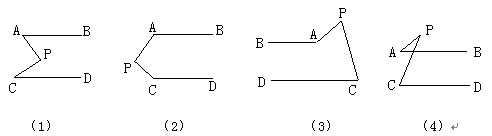

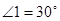 ,
,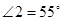 ,则
,则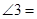 ;
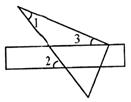
;
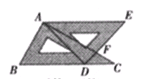
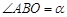 ,
,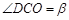 ,则
,则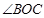 的度数是( )
的度数是( )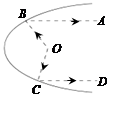
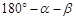
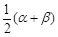
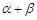
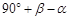
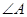 =
=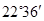 ,则
,则