题目内容
【题目】如图,ABCD的对角线AC、BD相交于点O,AE=CF. 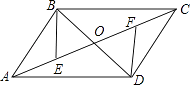
(1)求证:△BOE≌△DOF;
(2)连接DE、BF,若BD⊥EF,试探究四边形EBDF的形状,并对结论给予证明.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO,
∵AE=CF,
∴AO﹣AE=CO﹣FO,
∴EO=FO,
在△BOE和△DOF中  ,
,
∴△BOE≌△DOF(SAS)
(2)证明:四边形EBDF为菱形,等三角形的判定,以及菱形的判定,关键是掌握
理由:∵BO=DO,FO=EO,
∴四边形BEDF是平行四边形,
∵BD⊥EF,
∴四边形EBDF为菱形.

【解析】(1)根据平行四边形的性质可得BO=DO,AO=CO,再利用等式的性质可得EO=FO,然后再利用SAS定理判定△BOE≌△DOF即可;(2)根据BO=DO,FO=EO可得四边形BEDF是平行四边形,再根据对角线互相垂直的平行四边形是菱形可得四边形EBDF为菱形.

练习册系列答案
相关题目