题目内容
如图,二次函数 的图像交
的图像交 轴于
轴于 ,交
,交 轴于
轴于 ,过
,过 画直线。
画直线。
(1)求二次函数的解析式;
(2)若点P是抛物线上的动点,点Q是直线 上的动点,请判断是否存在以P、Q、O、C为顶点的四边形为平行四边形,若存在,请求出点Q的坐标;若不存在,请说明理由;
上的动点,请判断是否存在以P、Q、O、C为顶点的四边形为平行四边形,若存在,请求出点Q的坐标;若不存在,请说明理由;
(3)在 轴右侧的点
轴右侧的点 在二次函数图像上,以
在二次函数图像上,以 为圆心的圆与直线
为圆心的圆与直线 相切,切点为
相切,切点为 。且△CHM∽△AOC(点
。且△CHM∽△AOC(点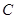 与点
与点 对应),求点
对应),求点 的坐标。
的坐标。
(1) (2)
(2) (2,2),
(2,2), (
(  ,
, ),
), (
( ,
, );
); (
( ,
, )。
)。
(3) 或
或
解析试题分析:解:(1)∵二次函数 的图像交
的图像交 轴于
轴于 ,∴设该二次函数的解析式为:
,∴设该二次函数的解析式为: ,又二次函数
,又二次函数 的图像交
的图像交 轴于
轴于 ,将
,将 代入,得
代入,得 ,解得,
,解得, ,∴抛物线的解析式为
,∴抛物线的解析式为 ,即
,即 ;
;
(2)若OC为平行四边形的边,设P( ,
, ),Q(
),Q( ,
, ),则PQ=
),则PQ= ,P、Q、O、C为顶点的四边形为平行四边形,则
,P、Q、O、C为顶点的四边形为平行四边形,则 ,∴
,∴ (舍去)
(舍去)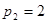 ,
, ,
, ;∴
;∴ (2,2),
(2,2), (
(  ,
, ),
), (
( ,
, );若OC为平行四边形的对角线,则
);若OC为平行四边形的对角线,则 (
( ,
, )。
)。
(3)∵△CHM∽△AOC,点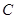 与点
与点 对应,∴
对应,∴ 

情形1:如上图,当 在点
在点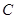 下方时,∵
下方时,∵
∴ 轴,∴
轴,∴ ,点
,点 在二次函数图像上,
在二次函数图像上,
∴ ,解得
,解得 (舍去)或
(舍去)或 ,∴
,∴ ;
;
情形2:如图,当 在点
在点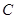 上方时,∵
上方时,∵ ,设
,设 交
交 轴于点P,设
轴于点P,设 ,则
,则 ,在
,在 中,
中,
由勾股定理,得 ,解得,
,解得, ,即
,即 ,
, 为直线
为直线 与抛物线的另一交点,设直线
与抛物线的另一交点,设直线 的解析式为
的解析式为 ,把
,把 的坐标代入,得
的坐标代入,得 ,解得,
,解得, ,∴
,∴ ,由
,由 ,解得,
,解得, (舍去)或
(舍去)或
此时 ,∴
,∴ ,∴点
,∴点 的坐标为
的坐标为 或
或
考点:二次函数在几何中的应用
点评:该题需要考虑的情况有多种,这是难点,需要学生经常练习,积累经验,结合图形找出突破口。

练习册系列答案
相关题目
 的图像交
的图像交 轴于
轴于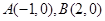 ,交
,交 轴于
轴于 ,过
,过 画直线。
画直线。
 在
在 ,求
,求 的长;
的长; 在二次函数图像上,以
在二次函数图像上,以 相切,切点为
相切,切点为 。
。 (点
(点 与点
与点 对应),求点
对应),求点 的半径为
的半径为 ,求点
,求点 的图像过点
的图像过点 ,与
,与 轴交于点
轴交于点 .
.
 (其中
(其中 是原点);
是原点); ,使
,使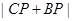 的值最小;
的值最小; 是线段
是线段 上的一个动点(不与
上的一个动点(不与 、
、 重合),过
重合),过 轴于
轴于 、
、 两点 . 请问
两点 . 请问 . 若存在,
. 若存在, 的图像交
的图像交 轴于
轴于 ,交
,交 轴于
轴于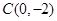 ,过
,过 画直线。
画直线。
 上的动点,请判断是否存在以P、Q、O、C为顶点的四边形为平行四边形,若存在,请求出点Q的坐标;若不存在,请说明理由;
上的动点,请判断是否存在以P、Q、O、C为顶点的四边形为平行四边形,若存在,请求出点Q的坐标;若不存在,请说明理由; 在二次函数图像上,以
在二次函数图像上,以 相切,切点为
相切,切点为 。且△CHM∽△AOC(点
。且△CHM∽△AOC(点 与点
与点 对应),求点
对应),求点 的图像与
的图像与 轴正半轴相交,其顶点坐标为(
轴正半轴相交,其顶点坐标为( ),下列结论:①
),下列结论:① ;②
;② ;③
;③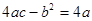 ;④
;④ .
.