题目内容
一个直角三角形两条直角边的长分别为6cm,8cm,则这个直角三角形的内心与外心之间的距离是分析:利用在Rt△ABC,可求得AB=10cm,根据内切圆的性质可判定四边形OECE是正方形,所以用r分别表示:CE=CD=r,AE=AN=6-r,BD=BN=8-r;再利用AB作为相等关系求出r=2cm,则可得AN=4cm,N为圆与AB的切点,M为AB的中点,根据直角三角形中外接圆的圆心是斜边的中点,即M为外接圆的圆心;在Rt△OMN中,先求得MN=AM-AN=1cm,由勾股定理可求得OM=
cm.
| 5 |
解答: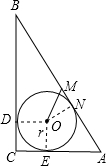 解:如图,在Rt△ABC,∠C=90°,AC=8cm,BC=6cm,
解:如图,在Rt△ABC,∠C=90°,AC=8cm,BC=6cm,
∴AB=10cm,
设Rt△ABC的内切圆的半径为r,则OD=OE=r,
∵∠C=90°,
∴CE=CD=r,AE=AN=6-r,BD=BN=8-r,
∴8-r+6-r=10,
解得r=2cm,
∴AN=4cm,
在Rt△OMN中,MN=AM-AN=1cm,
∴OM=
cm.
 解:如图,在Rt△ABC,∠C=90°,AC=8cm,BC=6cm,
解:如图,在Rt△ABC,∠C=90°,AC=8cm,BC=6cm,∴AB=10cm,
设Rt△ABC的内切圆的半径为r,则OD=OE=r,
∵∠C=90°,
∴CE=CD=r,AE=AN=6-r,BD=BN=8-r,
∴8-r+6-r=10,
解得r=2cm,
∴AN=4cm,
在Rt△OMN中,MN=AM-AN=1cm,
∴OM=
| 5 |
点评:此题考查了直角三角形的外心与内心概念,及内切圆的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
 不妨设
不妨设 ,三条边上的对应高分别为
,三条边上的对应高分别为 ,内接正方形的边长分别为
,内接正方形的边长分别为 .若你对本小题证明有困难,可直接用“
.若你对本小题证明有困难,可直接用“ ”这个结论,但在证明正确的情况下扣1分).
”这个结论,但在证明正确的情况下扣1分).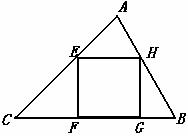
 形的内接正方形的有关问题进行了探讨:
形的内接正方形的有关问题进行了探讨: 同学的结果正确吗?若不正确,请举出一个反例并通过计算给予说明,若正确,请给出证明;
同学的结果正确吗?若不正确,请举出一个反例并通过计算给予说明,若正确,请给出证明; C的三条边分别为
C的三条边分别为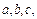 不妨设
不妨设 ,三条边上的对应高分别为
,三条边上的对应高分别为 ,内接正方形的边长分别为
,内接正方形的边长分别为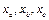 .若你对本小题证明有困难,可直接用
.若你对本小题证明有困难,可直接用 “
“ ”这个结论,但在证明正确的情况下扣1分).
”这个结论,但在证明正确的情况下扣1分).