题目内容
如图,AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,则∠BOC= 度.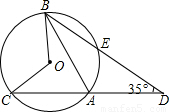
【答案】分析:在等腰△ABD中,根据三角形的外角性质可求出外角∠BAC的度数;而∠BAC、∠BOC是同弧所对的圆周角和圆心角,可根据圆周角和圆心角的关系求出∠BOC的度数.
解答:解:△ABD中,AB=AD,则:∠ABD=∠D=35°;
∴∠BAC=2∠D=70°;
∴∠BOC=2∠BAC=140°.
点评:此题主要考查了等腰三角形的性质、三角形的外角性质及圆周角定理的应用.
解答:解:△ABD中,AB=AD,则:∠ABD=∠D=35°;
∴∠BAC=2∠D=70°;
∴∠BOC=2∠BAC=140°.
点评:此题主要考查了等腰三角形的性质、三角形的外角性质及圆周角定理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
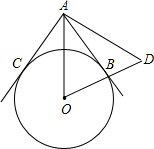 如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO等于( )
如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO等于( )| A、70° | B、64° | C、62° | D、51° |
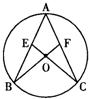
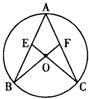 16、如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.
16、如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.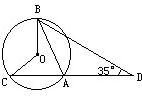 30、如图,AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,则∠BOC=
30、如图,AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,则∠BOC= 如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.求证:CE=BF.
如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.求证:CE=BF.