题目内容
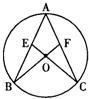
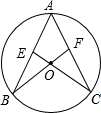 如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.求证:CE=BF.
如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.求证:CE=BF.分析:证明△BOE≌△COF,即可得到OE=OF,从而根据等式的性质得到CE=BF.
解答:解:∵在△BOE和△COF中,
,
∴△BOE≌△COF(ASA),
∴OE=OF,
又∵OB=OC
∴CE=BF.
|
∴△BOE≌△COF(ASA),
∴OE=OF,
又∵OB=OC
∴CE=BF.
点评:本题考查了圆的基本概念,以及全等三角形的判定与性质,正确证明两个三角形全等是关键.

练习册系列答案
相关题目
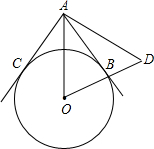 如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO等于( )
如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO等于( )| A、70° | B、64° | C、62° | D、51° |
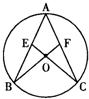 16、如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.
16、如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.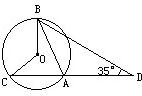 30、如图,AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,则∠BOC=
30、如图,AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,则∠BOC=