题目内容
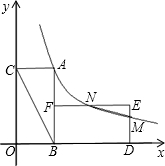 如图,面积为8的矩形ABOC的边OB、OC分别在x轴、y轴的正半轴上,点A在双曲线y=
如图,面积为8的矩形ABOC的边OB、OC分别在x轴、y轴的正半轴上,点A在双曲线y=| k | x |
(1)求k值;
(2)将矩形ABOC以B旋转中心,顺时针旋转90°后得到矩形FBDE,双曲线交DE于M点,交EF于N点,求△MEN的面积.
分析:(1)根据矩形的面积求出OC的长度,得到点A的坐标,然后利用待定系数法,把点A的坐标代入反比例函数解析式即可求出k值;
(2)根据矩形FBDE是由矩形ABOC旋转得到,然后求出点M、N、E的坐标,再根据点的坐标求出NE、ME的长度,然后根据三角形的面积公式计算即可求解.
(2)根据矩形FBDE是由矩形ABOC旋转得到,然后求出点M、N、E的坐标,再根据点的坐标求出NE、ME的长度,然后根据三角形的面积公式计算即可求解.
解答:解:(1)∵矩形ABOC的面积为8,且AC=2,
∴OC=4,
∵点A在第一象限,
∴A(2,4),
∵顶点A在双曲线y=
的图象上,
将A点代入双曲线函数中,得:k=xy=2×4=8,
即k=8;------------(4分)
(2)∵矩形ABOC以B为旋转中心,顺时针旋转90°后得到矩形BDEF,
∴点N、E纵坐标为2,点M、E横坐标为6,-----------(5分)
∴将y=2代入y=
中,得x=4,
将x=6代入y=
中,则y=
,
∴M(6,
),E(6,2),N(4,2),------------(8分)
∴EM=
,EN=2,
∴S△MEN=
×2×
=
.-------------(10分)
∴OC=4,
∵点A在第一象限,
∴A(2,4),
∵顶点A在双曲线y=
| k |
| x |
将A点代入双曲线函数中,得:k=xy=2×4=8,
即k=8;------------(4分)
(2)∵矩形ABOC以B为旋转中心,顺时针旋转90°后得到矩形BDEF,
∴点N、E纵坐标为2,点M、E横坐标为6,-----------(5分)
∴将y=2代入y=
| 8 |
| x |
将x=6代入y=
| 8 |
| x |
| 4 |
| 3 |
∴M(6,
| 4 |
| 3 |
∴EM=
| 2 |
| 3 |
∴S△MEN=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
点评:此题主要考查了反比例函数与一次函数的综合应用,根据矩形的面积求出OC的长度从而得到点A的坐标是解题的关键.

练习册系列答案
相关题目
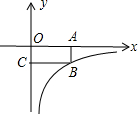 如图,面积为3的矩形OABC的一个顶点B在反比例函数y=
如图,面积为3的矩形OABC的一个顶点B在反比例函数y= 如图,面积为8的矩形ABOC的边OB、OC分别在x轴、y轴的正半轴上,点A在双曲线
如图,面积为8的矩形ABOC的边OB、OC分别在x轴、y轴的正半轴上,点A在双曲线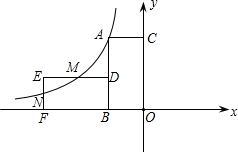 ,顶点A在双曲线y=
,顶点A在双曲线y= 轴、
轴、 轴的正半轴上,点A在双曲线
轴的正半轴上,点A在双曲线 的
的
 值;
值;