Question

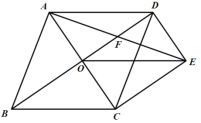
【题目】如图，在□ABCD中，对角线AC、BD相交于点O，且OA=OB．

（1）求证：四边形ABCD是矩形；

（2）若AB=6，∠AOB=120°，求BC的长．

Answer 1

【答案】（1）见解析；（2）2．

【解析】试题分析：（1）根据平行四边形的性质求出AO=OC，BO=OD，求出AC=BD，根据矩形的判定推出即可；

（2）根据矩形性质求出∠ABC=90°，求出∠CAB=30°，解直角三角形求出即可．

试题解析：（1）证明：∵四边形ABCD是平行四边形，

∴AO=OC，BO=OD，

∵OA=OB，

∴OA=OB=OC=OD，

∴AC=BD，

∴四边形ABCD是矩形；

（2）解：∵∠AOB=120°，OA=OB，

∴∠OAB=∠OBA=30°，

∵四边形ABCD是矩形，

∴∠ABC=90°，

∴AC=2BC，

∴AB= ，

∴BC=AB=6×=2．