题目内容
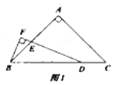
【题目】△ABC内接于⊙O,AB=AC,BD⊥AC,垂足为点D,交⊙O于点E,连接AE.
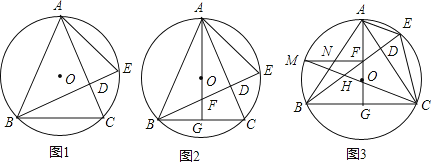
(1)如图1,求证:∠BAC=2∠CAE;
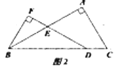
(2)如图2,射线AO交线段BD于点F,交BC边于点G,连接CE,求证:BF=CE;
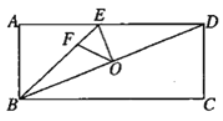
(3)如图3,在(2)的条件下,连接CO并延长,交线段BD于点H,交⊙O于点M,连接FM,交AB边于点N,若BH=DH,四边形BHOG的面积为5![]() ,求线段MN的长.
,求线段MN的长.
【答案】(1)见详解;(2)见详解;(3)![]()
【解析】
(1)先依据等腰三角形的性质和三角形的内角和定理证明∠BAC+2∠C=180°,然后得到2∠CAE+2∠E=180°,然后根据同弧所对的圆周角相等得到∠E=∠C,即可得到结论;
(2)连接OB、OC.先依据SSS证明△ABO≌△ACO,从而得到∠BAO=∠CAO,然后在依据ASA证明△ABF≌△ACE,最后根据全等三角形的性质可证明BF=CE;
(3)连接HG、BM.由三线合一的性质证明BG=CG,从而得到HG是△BCD的中位线,则∠FHO=∠AFD=∠HFO,于是可得到HO=OF,然后得到∠OGH=∠OHG,从而得到OH=OG,则OF=OG,接下来证明四边形MFGB是矩形,然后由MF∥BC证明△MFH∽△CBH,从而可证明HF=FD.接下来再证明△ADF≌△GHF,由全等三角形的性质的到AF=FG,然后再证明△MNB≌△NAF,于是得到MN=NF.设S△OHF=S△OHG=a,则S△FHG=2a,S△BHG=4a,然后由S四边形BHOG=5![]() ,可求得a=
,可求得a=![]() ,设HF=x,则BH=2x,然后证明△GFH∽△BFG,由相似三角形的性质可得到HG=
,设HF=x,则BH=2x,然后证明△GFH∽△BFG,由相似三角形的性质可得到HG=![]() x,然后依据S△BHG=
x,然后依据S△BHG=![]() BHHG=4
BHHG=4![]() ,可求得x=2,故此可得到HB、GH的长,然后依据勾股定理可求得BG的长,于是容易求得MN的长.
,可求得x=2,故此可得到HB、GH的长,然后依据勾股定理可求得BG的长,于是容易求得MN的长.
解:(1)∵AB=AC,
∴∠ABC=∠ACB.
∴∠BAC+2∠C=180°.
∵BD⊥AC,
∴∠ADE=90°.
∴∠E+∠CAE=90°.
∴2∠CAE+2∠E=180°.
∵∠E=∠ACB,
∴2∠CAE+2∠ACB=180°.
∴∠BAC=2∠CAE.
(2)连接OB、OC.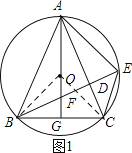
∵AB=AC,AO=AO,OB=OC,
∴△ABO≌△ACO.
∴∠BAO=∠CAO.
∵∠BAC=2∠CAE,
∴∠BAO=∠CAE.
在△ABF和△ACE中,
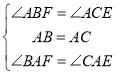 ,
,
∴△ABF≌△ACE.
∴BF=CE.
(3)连接HG、BM.
∵AB=AC,∠BAO=∠CAO,
∴AG⊥BC,BG=CG.
∵BH=DH,
∴HG是△BCD的中位线.
∴HG∥CD.
∴∠GHF=∠CDE=90°.
∵OA=OC,
∴∠OAC=∠OCA.
∵∠OAC+∠AFD=90°,∠OCA+∠FHO=90°,
∴∠FHO=∠AFD=∠HFO.
∴HO=OF.
∵∠HFO+∠OGH=90°,∠OHF+∠OH=90°,
∴∠OGH=∠OHG.
∴OH=OG.
∴OF=OG.
∵OM=OC,
∴四边形MFCG是平行四边形.
又∵MC是圆O的直径,
∴∠CBM=90°.
∴四边形MFGB是矩形.
∴MB=FG,∠FMB=∠AFN=90°.
∵MF∥BC,
∴△MFH∽△CBH.
∴![]() .
.
∴HF:HD=1:2.
∴HF=FD.
在△ADF和△GHF中,
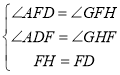 ,
,
∴△ADF≌△GHF.
∴AF=FG.
∴MB=AF.
在△MNB和△NAF中,
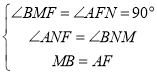 ,
,
∴△MNB≌△NAF.
∴MN=NF.
设S△OHF=S△OHG=a,则S△FHG=2a,S△BHG=4a,
∴S四边形BHOG=5a=5![]() .
.
∴a=![]() .
.
设HF=x,则BH=2x.
∵∠HHG=∠GFB,∠GHF=∠FGB,
∴△GFH∽△BFG.
∴![]() ,即
,即![]() .
.
∴HG=![]() .
.
∴S△BHG=![]() BHHG=
BHHG=![]() ×2x
×2x![]() =4
=4![]() ,
,
解得:x=2.
∴HB=4,GH=2![]() .
.
由勾股定理可知:BG=2![]() .
.
∴MF=2![]() .
.
∴MN=NF=![]() .
.

 字词句段篇系列答案
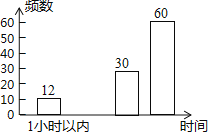
字词句段篇系列答案【题目】某市教育主管部门为了解学生的作业量情况,随机抽取了几所中学八年级的部分学生进行了一次调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图、表中所提供的信息解答下列问题:
(1)本次共抽取了 名学生进行调查;
(2)x= ,y= ,补全条形统计图;
(3)若这几所中学八年级的学生共有3200人,请估计做作业时间在2小时以上的学生人数是多少?
(4)由图表可知,这次被调查的八年级学生的作业时间的中位数一定落在1.5小时﹣2小时这一时段内,你认为这种判断正确吗?(不需要说明理由)
写作业时间 | 频数 | 频率 |
1小时以内 | 12 | 0.1 |
1﹣1.5 | x | 0.15 |
1.5﹣2 | 30 | 0.25 |
2小时以上 | 60 | y |
【题目】![]() 城有肥料
城有肥料![]() ,
,![]() 城有肥料
城有肥料![]() .现要把这些肥料全部运往
.现要把这些肥料全部运往![]() 、
、![]() 两乡,
两乡,![]() 乡需要肥料240t,
乡需要肥料240t,![]() 乡需要肥料
乡需要肥料![]() ,其运往
,其运往![]() 、
、![]() 两乡的运费如下表:
两乡的运费如下表:
两城/两乡 | C/(元/ | D/(元/ |
| 20 | 24 |
| 15 | 17 |
设从![]() 城运往
城运往![]() 乡的肥料为
乡的肥料为![]() ,从
,从![]() 城运往两乡的总运费为
城运往两乡的总运费为元,从
![]() 城运往两乡的总运费为
城运往两乡的总运费为![]() 元
元
(1)分别写出![]() 、
、![]() 与
与![]() 之间的函数关系式(不要求写自变量的取值范围);
之间的函数关系式(不要求写自变量的取值范围);
(2)试比较![]() 、
、![]() 两城总运费的大小;
两城总运费的大小;
(3)若![]() 城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.
城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.