题目内容
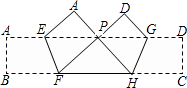
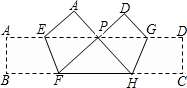
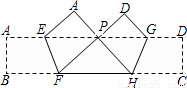
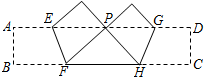 17、如图,把矩形纸条ABCD沿EF、GH同时折叠,B、C两点恰好落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则矩形ABCD的边BC长为
17、如图,把矩形纸条ABCD沿EF、GH同时折叠,B、C两点恰好落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则矩形ABCD的边BC长为
24
.分析:由图形翻折变换的性质可知,BF=PF,PH=CH,由于∠FPH=90°,所以在Rt△PFH中利用勾股定理可求出FH的长,进而可求出BC的长.
解答:解:∵矩形纸条ABCD沿EF、GH同时折叠,B、C两点恰好落在AD边的P点处,
∴BF=PF=8,PH=CH=6,
∵∠FPH=90°,
∴在Rt△PFH中,FH2=PF2+PH2,即FH2=82+62,
∴FH=10,
∴BC=BF+CH+FH=8+6+10=24.
故答案为:24.
∴BF=PF=8,PH=CH=6,
∵∠FPH=90°,
∴在Rt△PFH中,FH2=PF2+PH2,即FH2=82+62,
∴FH=10,
∴BC=BF+CH+FH=8+6+10=24.
故答案为:24.
点评:本题考查的是图形翻折变换的性质,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目