题目内容
求下列图形中阴影部分的面积.
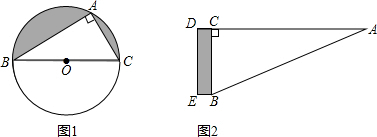
(1)如图1,AB=8,AC=6;
(2)如图2,AB=13,AD=14,CD=2.

(1)如图1,AB=8,AC=6;
(2)如图2,AB=13,AD=14,CD=2.
分析:(1)首先利用勾股定理计算出BC的长,进而得到圆的半径BO长,再利用半圆的面积减去直角三角形面积即可;
(2)首先计算出AC的长,再利用勾股定理计算出BC的长,然后利用矩形的面积公式计算即可.
(2)首先计算出AC的长,再利用勾股定理计算出BC的长,然后利用矩形的面积公式计算即可.
解答:解:(1)∵AB=8,AC=6,
∴BC=
=
=10,
∴BO=5,
∵S△ABC=
AB×AC=
×8×6=24,
S半圆=
π×52=
,
∴S阴影=
-24;
(2)∵AD=14,CD=2,
∴AC=12,
∵AB=13,
∴CB=
=
=5,
∴BC=
| AB2+CA2 |
| 64+36 |
∴BO=5,
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
S半圆=
| 1 |
| 2 |
| 25π |
| 2 |
∴S阴影=
| 25π |
| 2 |
(2)∵AD=14,CD=2,
∴AC=12,
∵AB=13,
∴CB=
| AB2-AC2 |
| 169-144 |
点评:此题主要考查了勾股定理,关键是熟练掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目

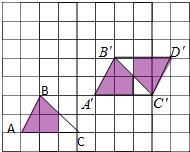 如图,在方格纸(每个小方格都是边长为1个单位长度的正方形)上,并且图形的顶点均在格点上,请结合所给的方格纸解答下列问题:
如图,在方格纸(每个小方格都是边长为1个单位长度的正方形)上,并且图形的顶点均在格点上,请结合所给的方格纸解答下列问题: