题目内容
 三角形ABC是等边三角形(三条边相等的三角形)表示其边长的代数式已在图中标出,则2(x2+y2-xy-7)的值为
三角形ABC是等边三角形(三条边相等的三角形)表示其边长的代数式已在图中标出,则2(x2+y2-xy-7)的值为156.16
156.16
.分析:由等边三角形的三边相等,可列方程,从而求得x、y的值,再把值代入所求分式即可求解.
解答:解:由等边三角形的三边相等,可得
,
解得
.
故原式=2×(6.22+10.62-6.2×10.6-7)
=2×(38.44+112.36-65.72-7)
=2×78.08
=156.16.
故2(x2+y2-xy-7)的值为156.16.
故答案为:156.16.
|
解得
|
故原式=2×(6.22+10.62-6.2×10.6-7)
=2×(38.44+112.36-65.72-7)
=2×78.08
=156.16.
故2(x2+y2-xy-7)的值为156.16.
故答案为:156.16.
点评:此题考查二元一次方程组的应用,同时利用了等边三角形的性质列方程,难点在于代入计算比较繁琐,需仔细答题.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明. (2013•鼓楼区一模)已知A、B、C三点均在⊙O上,且△ABC是等边三角形.
(2013•鼓楼区一模)已知A、B、C三点均在⊙O上,且△ABC是等边三角形.
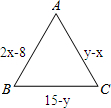 三角形ABC是等边三角形(三条边相等的三角形)表示其边长的代数式已在图中标出,则2(x2+y2-xy-7)的值为________.
三角形ABC是等边三角形(三条边相等的三角形)表示其边长的代数式已在图中标出,则2(x2+y2-xy-7)的值为________.