题目内容
 (2013•鼓楼区一模)已知A、B、C三点均在⊙O上,且△ABC是等边三角形.
(2013•鼓楼区一模)已知A、B、C三点均在⊙O上,且△ABC是等边三角形.(1)如图,用直尺和圆规作出△ABC;(不写作法,保留作图痕迹)
(2)若点P是
 | BC |
分析:(1)首先把圆六等分,再隔一个点取一点,作出等边三角形即可;
(2)在PA上取点D,使得PD=PC,连接CD.首先证明△PCD是等边三角形,进而得出△CAD≌△CBP,即可得出答案.
(2)在PA上取点D,使得PD=PC,连接CD.首先证明△PCD是等边三角形,进而得出△CAD≌△CBP,即可得出答案.
解答: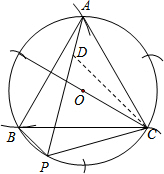 解:(1)如图;
解:(1)如图;
(2)PA=PB+PC.理由如下:
如图,在PA上取点D,使得PD=PC,连接CD.
∵△ACB是等边三角形,
∴AB=BC=CA,∠APC=∠ABC=60°.
∴△PCD是等边三角形.
∴CD=CP.
∵∠ACD+∠DCB=60°,
∠BCP+∠DCB=60°,
∴∠ACD=∠BCP,
在△CAD和△CBP中
∴△CAD≌△CBP(ASA).
∴AD=BP.
∴PA=PD+AD=PB+PC.
 解:(1)如图;
解:(1)如图;(2)PA=PB+PC.理由如下:
如图,在PA上取点D,使得PD=PC,连接CD.
∵△ACB是等边三角形,
∴AB=BC=CA,∠APC=∠ABC=60°.
∴△PCD是等边三角形.
∴CD=CP.
∵∠ACD+∠DCB=60°,
∠BCP+∠DCB=60°,
∴∠ACD=∠BCP,
在△CAD和△CBP中
|
∴△CAD≌△CBP(ASA).
∴AD=BP.
∴PA=PD+AD=PB+PC.
点评:此题主要考查了等边三角形的作法以及全等三角形的判定与性质等知识,得出△CAD≌△CBP是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目