题目内容
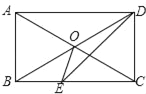
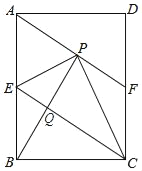
【题目】如图,在矩形ABCD中,点E是边AB的中点,△EBC沿直线EC翻折,使B点落在矩形ABCD内部的点P处,联结AP并延长AP交CD于点F,联结BP交CE于点Q.
(1)求证:四边形AECF是平行四边形;
(2)如果PA=PE,求证:△APB≌△EPC.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)由折叠的性质得到BE=PE,EC与PB垂直,根据E为AB中点,得到AE=EB=PE,利用三角形内一边上的中线等于这条边的一半的三角形为直角三角形,得到∠APB为90°,进而得到AF与EC平行,再由AE与FC平行,利用两对边平行的四边形为平行四边形即可得证;
(2)根据三角形AEP为等边三角形,得到三条边相等,三内角相等,再由折叠的性质及邻补角定义得到一对角相等,根据同角的余角相等得到一对角相等,再由AP=EB,利用AAS即可得证.
证明:(1)由折叠得到EC垂直平分BP,
设EC与BP交于Q,
∴BQ=PQ
∵E为AB的中点,
∴AE=EB,
∴EQ为△ABP的中位线,
∴AF∥EC,
∵AE∥FC,
∴四边形AECF为平行四边形;
(2)∵AF∥EC,
∴∠APB=∠EQB=90°,
由翻折性质∠EPC=∠EBC=90°,∠PEC=∠BEC,
∵E为直角△APB斜边AB的中点,且AP=EP,
∴△AEP为等边三角形,∠BAP=∠AEP=60°,
∠CEP=∠CEB=![]() =60°,
=60°,
在△ABP和△EPC中,
∠BAP=∠CEP
∠APB=∠EPC
AP=EP
∴△ABP≌△EPC(AAS).

 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】2019年中国北京世界园艺博览会已于2019年4月29日在北京市延庆区开展,吸引了大批游客参观游览.五一小长假期间平均每天入园人数大约是8万人,佳佳等5名同学组成的学习小组,随机调查了五一假期中入园参观的部分游客,获得了他们在园内参观所用时间,并对数据进行整理,描述和分析,下面给出了部分信息:
a.参观时间的频数分布表如下:
时间 | 频数(人数) | 频率 |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
合计 |
| 1.000 |
b.参观时间的频数分布直方图如图:
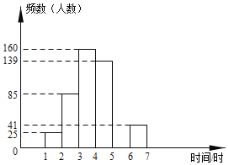
根据以上图表提供的信息,解答下列问题:
(1)这里采用的调查方式是 ;
(2)表中![]() ,
,![]() ,
,![]() ;
;
(3)并请补全频数分布直方图;
(4)请你估算五一假期中平均每天参观时间小于4小时的游客约有多少万人?