题目内容
如图，在直角梯形ACED中，∠C=∠E=90°，BC=DE，AC=BE．设BC=a，AC=b，AB=c，试利用该图形证明勾股定理．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
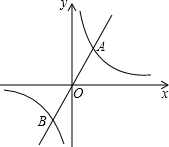如图，正比例函数y1=k1x和反比例函数y2=| k2 |
| x |
①k1＜k2；
②当x＜-1时，y1＜y2；
③当y1＞y2时，x＞1；
④当x＜0时，y2随x的增大而减小．
其中正确的有（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
如图，Rt△ABC中，∠C=90°，AC=3，BC=4．分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC，四块阴影部分的面积分别为S1、S2、S3、S4． 则S1+S2+S3+S4等于（ ）| A、14 | B、16 | C、18 | D、20 |
四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”（如图）．如果小正方形面积为49，大正方形面积为169，直角三角形中较小的锐角为θ，那么sinθ的值是
小华把如图所示的4×4的方格或分成4个完全相同的直角三角形（Ⅰ，Ⅱ，Ⅲ，Ⅳ），然后将这4个直角三角形拼成图（2），你能帮他求出图（2）中最大正方形的边长吗？边长是整数吗？若不是整数，那么请你估计这个边长的值在哪两个整数之间？下列四组线段中，可以构成直角三角形的是（ ）
| A、4，5，6 | ||
| B、1.5，2，2.5 | ||
| C、2，3，4 | ||
D、1，
|
如图，AC是电杆的一根拉线，测得BC=6米，∠ACB=60°，则AB的长为（ ）| A、12米 | ||
B、6
| ||
| C、6米 | ||
D、2
|
若△ABC的面积是8cm2，则它的三条中位线围成的三角形的面积是（ ）
| A、2cm2 | B、4cm2 | C、6cm2 | D、无法确定 |
如图，A、B分别是x轴、y轴的正半轴上的两个动点，点P是AB的中点，且OP=2，则△AOB的面积的最大值为（ ）