Question

【题目】探究：

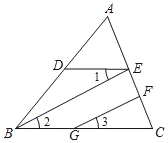
如图①，在△ABC中，点D、E、F分别在边AB、AC、CB上，且DE∥BC，EF∥AB，若∠ABC＝65°，求∠DEF的度数．请将下面的解答过程补充完整，并填空(理由或数学式)：

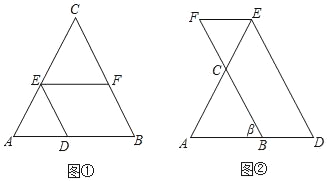
解：∵DE∥BC(　 　)

∴∠DEF＝　 　(　 　)

∵EF∥AB

∴　 　＝∠ABC(　 　)

∴∠DEF＝∠ABC(　 　)

∵∠ABC＝65°

∴∠DEF＝　 　

应用：

如图②，在△ABC中，点D、E、F分别在边AB、AC、BC的延长线上，且DE∥BC，EF∥AB，若∠ABC＝β，则∠DEF的大小为　 　(用含β的代数式表示)．

Answer 1

【答案】探究：见解析；应用：见解析.

【解析】

探究：依据两直线平行，内错角相等以及两直线平行，同位角相等，即可得到∠DEF＝∠ABC，进而得出∠DEF的度数．应用：依据两直线平行，同位角相等以及两直线平行，同旁内角互补，即可得到∠DEF的度数．

解：探究：∵DE∥BC（已知）

∴∠DEF＝∠CFE（两直线平行，内错角相等）

∵EF∥AB

∴∠CFE＝∠ABC（两直线平行，同位角相等）

∴∠DEF＝∠ABC（等量代换）

∵∠ABC＝65°

∴∠DEF＝65°

故答案为：已知；∠CFE；两直线平行，内错角相等；∠CFE；两直线平行，同位角相等；等量代换；65°．

应用：∵DE∥BC

∴∠ABC＝∠D＝β

∵EF∥AB

∴∠D+∠DEF＝180°

∴∠DEF＝180°﹣∠D＝180°﹣β，

故答案为：180°﹣β．