题目内容
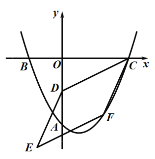
【题目】如图,在平面直角坐标系中,OABC的顶点B、C在第二象限,点D为AB边的中点,反比例函数y=![]() 在第二象限的图象经过C、D两点.若点A的坐标是(﹣2
在第二象限的图象经过C、D两点.若点A的坐标是(﹣2![]() ,0),tan∠COA=3,则k的值为_____.
,0),tan∠COA=3,则k的值为_____.
【答案】-16
【解析】
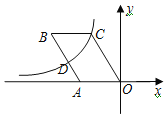
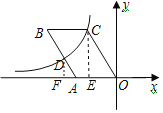
过点C作CE⊥OA于E,过点D作DF⊥x轴于F,依据△ADF∽△OCE,可得CE=2DF,OE=2AF,设OE=a,可得CE=3a,C(-a,3a),D(﹣![]() a﹣
a﹣![]() ,
,![]() a),依据反比例函数y=
a),依据反比例函数y=![]() 在第二象限的图象经过C、D两点,即可得到a的值,进而得出k的值.
在第二象限的图象经过C、D两点,即可得到a的值,进而得出k的值.
如图,过点C作CE⊥OA于E,过点D作DF⊥x轴于F,则∠AFD=∠OEC=90°,
∵OC∥AB,
∴∠DAF=∠COE,
∴△ADF∽△OCE,
在![]() OABC中,OC=AB,D为边AB的中点,
OABC中,OC=AB,D为边AB的中点,
∴OC=AB=2AD,
∴CE=2DF,OE=2AF,
设OE=a,则CE=3a,C(﹣a,3a),
∴AF=![]() a,DF=
a,DF=![]() a,
a,
又∵A(![]() ,0),
,0),
∴AO=![]() ,
,
∴OF=![]() a+
a+![]() ,
,
∴D(﹣![]() a﹣
a﹣![]() ,
,![]() a),
a),
∵反比例函数y=![]() 在第二象限的图象经过C、D两点,
在第二象限的图象经过C、D两点,
∴k=﹣a3a=(﹣![]() a﹣
a﹣![]() )
)![]() a,
a,
解得a=![]() ,
,
∴k=﹣![]() ×
×![]() =﹣16
=﹣16
故答案为:﹣16

【题目】“全民防控新冠病毒”期间某公司推出一款消毒产品,成本价8元/千克,经过市场调查,该产品的日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
(元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
销售单价 | 12 | 16 | 20 | 24 |
日销售量 | 220 | 180 | 140 |
|
(注:日销售利润![]() 日销售量
日销售量![]() (销售单价
(销售单价![]() 成本单价)
成本单价)
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出
的函数解析式(不要求写出![]() 的取值范围);
的取值范围);
(2)根据以上信息,填空:
①![]() _______千克;
_______千克;
②当销售价格![]() _______元时,日销售利润
_______元时,日销售利润![]() 最大,最大值是_______元;
最大,最大值是_______元;
(3)该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象,为了保证捐赠后每天的剩余利润不低于1500元,试确定该产品销售单价的范围.