题目内容
(2005•日照)如图,△OAB是边长为4+2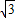 的等边三角形,其中O是坐标原点,顶点B在y轴的正半轴上.将△OAB折叠,使点A与OB边上的点P重合,折痕与OA、AB的交点分别是E、F.如果PE∥x轴,
的等边三角形,其中O是坐标原点,顶点B在y轴的正半轴上.将△OAB折叠,使点A与OB边上的点P重合,折痕与OA、AB的交点分别是E、F.如果PE∥x轴,(1)求点P、E的坐标;
(2)如果抛物线y=-
 x2+bx+c经过点P、E,求抛物线的解析式.
x2+bx+c经过点P、E,求抛物线的解析式.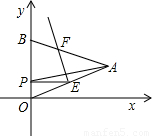
【答案】分析:(1)求E点的坐标就要求出OP,PE的值,在直角三角形OPE中,∠POE=60°,因此OE=2OP,PE=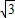 OP,而OA=OE+AE=2OP+
OP,而OA=OE+AE=2OP+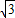 OP,据此可求出OP,OE,PE的长.由此求出P和E点的坐标.
OP,据此可求出OP,OE,PE的长.由此求出P和E点的坐标.
(2)将P、E的坐标代入抛物线中即可求出二次函数的解析式.
解答:解:(1)设OP=x,则OE=2x,PE=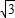 x.
x.
根据折叠的性质可得AE=PE=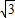 x,
x,
则有OA=OE+AE=OE+PE=2x+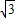 x=4+2
x=4+2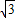 ,
,
∴x=2,
∴OP=2,PE=2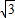 ,
,
因此P(0,2),E(2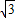 ,2);
,2);
(2)将P、E坐标代入抛物线可得:
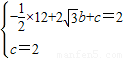 ,
,
解得: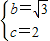 ,
,
∴抛物线的解析式为y=- x2+
x2+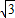 x+2.
x+2.
点评:本题着重考查了等边三角形的性质、图形旋转变换、待定系数法求二次函数解析式等重要知识点.
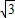 OP,而OA=OE+AE=2OP+
OP,而OA=OE+AE=2OP+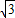 OP,据此可求出OP,OE,PE的长.由此求出P和E点的坐标.
OP,据此可求出OP,OE,PE的长.由此求出P和E点的坐标.(2)将P、E的坐标代入抛物线中即可求出二次函数的解析式.
解答:解:(1)设OP=x,则OE=2x,PE=
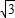 x.
x.根据折叠的性质可得AE=PE=
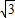 x,
x,则有OA=OE+AE=OE+PE=2x+
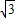 x=4+2
x=4+2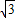 ,
,∴x=2,
∴OP=2,PE=2
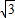 ,
,因此P(0,2),E(2
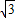 ,2);
,2);(2)将P、E坐标代入抛物线可得:
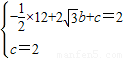 ,
,解得:
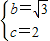 ,
,∴抛物线的解析式为y=-
 x2+
x2+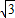 x+2.
x+2.点评:本题着重考查了等边三角形的性质、图形旋转变换、待定系数法求二次函数解析式等重要知识点.

练习册系列答案
相关题目
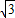 的等边三角形,其中O是坐标原点,顶点B在y轴的正半轴上.将△OAB折叠,使点A与OB边上的点P重合,折痕与OA、AB的交点分别是E、F.如果PE∥x轴,
的等边三角形,其中O是坐标原点,顶点B在y轴的正半轴上.将△OAB折叠,使点A与OB边上的点P重合,折痕与OA、AB的交点分别是E、F.如果PE∥x轴, x2+bx+c经过点P、E,求抛物线的解析式.
x2+bx+c经过点P、E,求抛物线的解析式.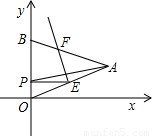
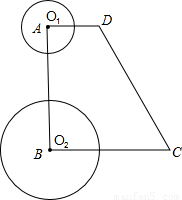
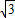 cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为t.
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为t.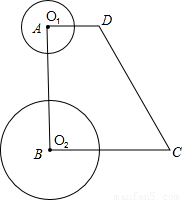
 ,PB=4.
,PB=4.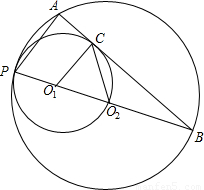
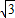 cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为t.
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为t.