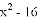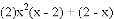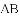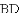如图.已知抛物线经过原点O和x轴上一点A(4.0).抛物线顶点为E.它的对称轴与x轴交于点D.直线y=-2x-1经过抛物线上一点B且与y 轴交于点C.与抛物线的对称轴交于点F.(1)求抛物线的解析式,是x轴上方抛物线上的一点.若S△ADP=S△ADC,求出所有符合条件的点P的坐标,(3)点Q是平面内任意一点.点M从点F出发.沿对称轴向上以每秒1个单位长度的速度匀速运动.设点M的运动时题目和参考答案——青夏教育精英家教网—

题目内容

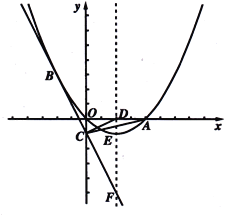
如图，已知抛物线经过原点O和x轴上一点A（4，0），抛物线顶点为E，它的对称轴与x轴交于点D.直线y=-2x-1经过抛物线上一点B（-2，m）且与y 轴交于点C，与抛物线的对称轴交于点F.

（1）求抛物线的解析式；

（2）P(x，y)是x轴上方抛物线上的一点，若S△ADP=S△ADC,求出所有符合条件的点P的坐标；

（3）点Q是平面内任意一点，点M从点F出发，沿对称轴向上以每秒1个单位长度的速度匀速运动，设点M的运动时间为t秒，是否能使以Q、A、E、M四点为顶点的四边形是菱形.若能，请求出点M的运动时间t的值；若不能，请说明理由.

练习册系列答案

相关题目

因式分解(1) 4

一个正n边形的每一个外角都是36°，则n=（　　）

A. 7 B. 8 C. 9 D. 10

计算：6﹣（3﹣5）=_____．

等腰三角形底角与顶角之间的函数关系是（　　）

A. 正比例函数 B. 一次函数 C. 反比例函数 D. 二次函数

如图，在边长为1的正方形组成的网格中，△ABC的顶点均在格点上，点A、B、C的坐标分别是A(-2，3)、B(-1，2)、C(-3，1)，将△ABC绕点O顺时针旋转90°后得到△A1B1C1.(点A、B、C的对应点分别是点A1、B1、C1)

(1)在正方形网格中作出△A1B1C1；

(2)直接写出点A1 的坐标为___________.

如图，AB为圆O的直径，CD为圆O的弦，AB⊥CD于M，若AB=10cm，CD=8cm，则AM=_________cm．

如图，张明同学想测量某铜像的高度，已知铜像（图中）高度比底座（图中）高度多1米，张明随后用高度为1米的测角仪（图中）测得铜像顶端点的仰角β＝51°24′，底座顶端点的仰角＝26°36′．请你帮助张明算出铜像AB的高度（把铜像和底座近似看在一条直线上它的抽象几何图形如左图）．（参考数据：sin26°36′≈0.45, cos26°36′≈0.89，tan26°36′≈0.5，sin51°24′≈0.78,cos51°24′≈0.6，tan51°24′≈1.25）

在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表：

跳高成绩(m)	1.50	1.55	1.60	1.65	1.70	1.75
跳高人数	1	3	2	3	5	1

这些运动员跳高成绩的中位数和众数分别是（）

A. 1.65，1.70 B. 1.70，1.65 C. 1.70，1.70 D. 3，5

试题分类