题目内容
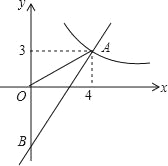
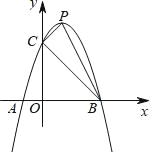
【题目】如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.
(1)求抛物线的解析式.
(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.
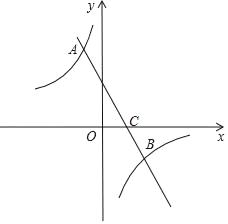
(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)①Q(2,3);②Q2(![]() ,
, ![]() ),Q3(
),Q3(![]() ,
,![]() );(3)存在点M,N使四边形MNED为正方形,MN=9
);(3)存在点M,N使四边形MNED为正方形,MN=9![]() 或
或![]() .理由见解析.
.理由见解析.
【解析】
(1)设出抛物线顶点坐标,把C坐标代入求出即可;
(2)由△BCQ与△BCP的面积相等,得到PQ与BC平行,①过P作作PQ∥BC,交抛物线于点Q,如图1所示;②设G(1,2),可得PG=GH=2,过H作直线Q2Q3∥BC,交x轴于点H,分别求出Q的坐标即可;
(3)存在点M,N使四边形MNED为正方形,如图2所示,过M作MF∥y轴,过N作NF∥x轴,过N作NH∥y轴,则有△MNF与△NEH都为等腰直角三角形,设M(x1,y1),N(x2,y2),设直线![]() 解析式为y=-x+b,与二次函数解析式联立,消去y得到关于x的一元二次方程,利用根与系数关系表示出NF2,由△MNF为等腰直角三角形,得到MN2=2NF2,若四边形MNED为正方形,得到NE2=MN2,求出b的值,进而确定出MN的长,即为正方形边长.
解析式为y=-x+b,与二次函数解析式联立,消去y得到关于x的一元二次方程,利用根与系数关系表示出NF2,由△MNF为等腰直角三角形,得到MN2=2NF2,若四边形MNED为正方形,得到NE2=MN2,求出b的值,进而确定出MN的长,即为正方形边长.
(1)设y=a(x﹣1)2+4(a≠0),
把C(0,3)代入抛物线解析式得:a+4=3,即a=﹣1,
则抛物线解析式为y=﹣(x﹣1)2+4=﹣x2+2x+3;
(2)由B(3,0),C(0,3),得到直线BC解析式为y=﹣x+3,
∵S△OBC=S△QBC,
∴PQ∥BC,
①过P作PQ∥BC,交抛物线于点Q,如图1所示,
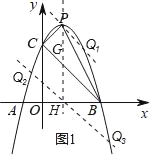
∵P(1,4),∴直线PQ解析式为y=﹣x+5,
联立得:![]() ,
,
解得:![]() 或
或![]() ,即Q(2,3);
,即Q(2,3);
②设G(1,2),∴PG=GH=2,
过H作直线Q2Q3∥BC,交x轴于点H,则直线Q2Q3解析式为y=﹣x+1,
联立得:![]() ,
,
解得: 或
或 ,
,
∴Q2(![]() ,
,![]() ),Q3(
),Q3(![]() ,
,![]() );
);
(3)存在点M,N使四边形MNED为正方形,
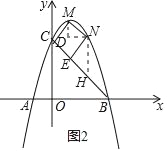
如图2所示,过M作MF∥y轴,过N作NF∥x轴,过N作NH∥y轴,则有△MNF与△NEH都为等腰直角三角形,
设M(x1,y1),N(x2,y2),设直线MN解析式为y=﹣x+b,
联立得:![]() ,
,
消去y得:x2﹣3x+b﹣3=0,
∴NF2=|x1﹣x2|2=(x1+x2)2﹣4x1x2=21﹣4b,
∵△MNF为等腰直角三角形,
∴MN2=2NF2=42﹣8b,
∵NH2=(b﹣3)2,∴NF2=![]() (b﹣3)2,
(b﹣3)2,
若四边形MNED为正方形,则有NE2=MN2,
∴42﹣8b=![]() (b2﹣6b+9),
(b2﹣6b+9),
整理得:b2+10b﹣75=0,
解得:b=﹣15或b=5,
∵正方形边长为MN=![]() ,
,
∴MN=9![]() 或
或![]() .
.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案