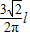题目内容
已知一弧长为l,所对的圆心角为120°,那么它所对的弦长为
- A.
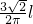
- B.
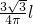
- C.
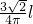
- D.
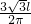
D
分析:先利用弧长公式计算出半径,然后再利用60°角的三角函数求出弦的长.
解答: 解:∵l
解:∵l =
=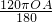 ,
,
∴OA= .
.
作OC⊥AB于C点,则∠AOC=60°;AC=BC= AB.
AB.
∴sin∠AOC=sin60°=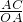 =
= ,
,
∴AC=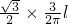 =
=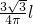 ,
,
∴弦AB=2AC=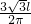 .
.
故选D.
点评:此题主要考查了弧长公式的运用、垂径定理及特殊角的三角函数值.
分析:先利用弧长公式计算出半径,然后再利用60°角的三角函数求出弦的长.
解答:
 解:∵l
解:∵l =
=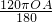 ,
,∴OA=
 .
.作OC⊥AB于C点,则∠AOC=60°;AC=BC=
 AB.
AB.∴sin∠AOC=sin60°=
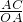 =
= ,
,∴AC=
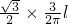 =
=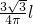 ,
,∴弦AB=2AC=
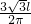 .
.故选D.
点评:此题主要考查了弧长公式的运用、垂径定理及特殊角的三角函数值.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
已知一弧长为l,所对的圆心角为120°,那么它所对的弦长为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|