题目内容
【题目】如图，将两块直角三角板的直角顶点C叠放在一起.
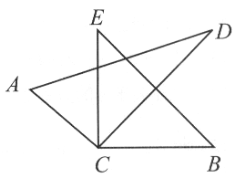
（1）若∠DCB=35°，求∠ACB的度数；
（2）若∠ACB=140°，求∠DCE的度数.
【答案】(1)∠ACB=125°；(2)∠ECD=40°.
【解析】
试题分析：（1）利用∠ACB=∠ACD+∠DCB，直接求出即可；
（2）首先求出∠DCB，进一步利用余角的意义解决问题．
试题解析：
（1）因为∠ACD＝90°，∠DCB=35°
所以∠ACB＝∠ACD+∠DCB
＝90°+35°
＝125°
（2）因为∠ACB=140°，∠ACD＝90°
所以∠DCB＝∠ACB－∠ACD
＝140°－90°
＝50°
又因为∠ECB＝90°
所以∠ECD＝∠ECB－∠DCB
＝90°－50°
＝40°
练习册系列答案
相关题目
【题目】已知：在Rt△ABC中，∠C＝90°，∠A、∠B、∠C的对边分别为a、b、c，设△ABC的面积为S，周长为l．
（1）填表：
三边a、b、c |
|
|
3、4、5 | 2 | |
5、12、13 | 4 | |
8、15、17 | 6 |
（2）如果
，观察上表猜想： 
(用含有m的代数式表示)．
（3）证明（2）中的结论．
