题目内容
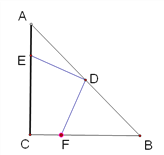
【题目】在△ABC中,∠ACB=900,AC=BC,D为AB中点.E、F分别从A、C同时出发,以每秒1个单位速度分别向C、B运动(分别到达C、B后停止运动)
(1)求证:①DE=DF;②DE⊥DF.
(2)若AB=![]() .运动时间为t.
.运动时间为t.
①求△AED面积S与t的函数关系式,并写出t的取值范围;
②若△BDF为等腰三角形,求t;
③连接EF,若EF最小,求t.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() ;③t=2
;③t=2
【解析】试题分析:(1)连接CD,利用边角边证![]() 即可;
即可;
(2)①利用三角形的面积公式即可列出函数关系式;
②分三种情况DF=DB,DF=BF,BD=BF进行讨论即可:
③由(1)可知, ![]() 为等腰直角三角形,当DE最小(即DE⊥AC)时,EF最小,即可求解.
为等腰直角三角形,当DE最小(即DE⊥AC)时,EF最小,即可求解.
解:(1)连接CD,
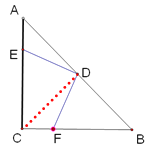
∵∠ACB=900,AC=BC,
∴△ABC是等腰直角三角形,
∴![]() ,
,
∵D为AB中点,
∴CD=AD=BD, ![]() ,
,
∴![]()
∵E、F分别从A、C同时出发,以每秒1个单位速度分别向C、B运动,
∴![]()
∴![]() ,
,
∴DE=DF, ![]() ,
,
∵![]()
∴DE⊥DF.
(2)作DM⊥AC垂足为M,则DM=![]() ,
,

∵AB=![]() ,且∠ACB=900,AC=BC,
,且∠ACB=900,AC=BC,
∴由勾股定理得![]() ,
,
∴DM=2,
∵AM=t,
∴![]()
即![]()
∴![]()
②有三种情况,
当DF=BD时,此时点F在C处,即![]()
当DF=BF时,此时点F在BC中点处,即![]()
当DB=BF时,BF=DB=![]() CF=
CF=![]() 即
即![]()
综上所述,当△BDF为等腰三角形时, t的值为![]() .
.
③当点E运动到AC中点时,EF最小,此时![]()

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目