题目内容
 香蕉味香、富于营养,常食香蕉不仅有益于大脑,预防神经疲劳,还有润肺止咳、防止便秘的作用.今年三月份从3月1日起,“欣欣”香蕉批发店日销售量y1(箱)与时间第x(天)的函数关系如下表:
香蕉味香、富于营养,常食香蕉不仅有益于大脑,预防神经疲劳,还有润肺止咳、防止便秘的作用.今年三月份从3月1日起,“欣欣”香蕉批发店日销售量y1(箱)与时间第x(天)的函数关系如下表:| 第x(天) | 1 | 2 | 3 | 4 | … |
| 日销售量y1(箱) | 22 | 24 | 26 | 28 | … |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出三月份日销售量y1(元)与时间第x(天)之间的函数关系式;观察右图,直接写出四月份日销售量y2(元)与时间第x(天)之间的一次函数关系式;
(2)请问第几天香蕉日销售利润W最大,最大日销售利润是多少元?
(3)进入五月,由于南海局势持续紧张,中国加强了对菲律宾香蕉进口的审查,市场上来自菲律宾的香蕉锐减,受此影响,与4月10日发生“黄岩岛事件”那天相比,5月10日该店的销售量下降了4a%,每千克售价提高了a%,成本增加了50%,5月10日的销售利润为3200元.请参考以下数据,计算出a的值(结果精确到0.1).
(参考数据:
| 42 |
| 41 |
| 40 |
分析:(1)待定系数法将(1,22),(2,24)代入y1=k1x+b1,即可求得三月份日销售量y1(元)与时间第x(天)之间的函数关系式;待定系数法将(41,80),(51,70)代入y2=k2x+b2,即可求得四月份日销售量y2(元)与时间第x(天)之间的一次函数关系式;
(2)首先分当1≤x≤31时,当32≤x≤61时两种情况表示出日销售利润,进而利用函数增减性求出最大利润;
(3)首先利用当x=41时,根据5月10日的销售利润为3200元,得出关于a的方程,进而求出a的值即可.
(2)首先分当1≤x≤31时,当32≤x≤61时两种情况表示出日销售利润,进而利用函数增减性求出最大利润;
(3)首先利用当x=41时,根据5月10日的销售利润为3200元,得出关于a的方程,进而求出a的值即可.
解答:解:(1)y1=2x+20(1≤x≤31),
y2=-x+121(32≤x≤61),
(2)当1≤x≤31时,w=(p1-2)•25y1=25(-0.1x+5)(2x+20)=-5(x-20)2+4500.
故当x=20时,w最大=4500.
当32≤x≤61时,w=(p2-2)•25y2=25(0.1x-1.1)(-x+121)=-2.5(x-66)2+7562.5.
又∵当x≤61时,w随x增大而增大,
∴当x=61时,w最大=7500.
又∵4500<7500,
∴当x=61时,w最大=7500.
答:第61天香蕉日销售利润W最大,最大日销售利润是7500元.
(3)当x=41时,y2=80,p2=5,则
[5(1+a%)-2(1+50%)]•80(1-40%)×25=3200,
令a%=t,则100t2+15t-2=0,
解得t=
≈
,
又∵t>0,
∴t≈0.085,
∴a≈8.5.
故a的值为8.5.
y2=-x+121(32≤x≤61),
(2)当1≤x≤31时,w=(p1-2)•25y1=25(-0.1x+5)(2x+20)=-5(x-20)2+4500.
故当x=20时,w最大=4500.
当32≤x≤61时,w=(p2-2)•25y2=25(0.1x-1.1)(-x+121)=-2.5(x-66)2+7562.5.
又∵当x≤61时,w随x增大而增大,
∴当x=61时,w最大=7500.
又∵4500<7500,
∴当x=61时,w最大=7500.
答:第61天香蕉日销售利润W最大,最大日销售利润是7500元.
(3)当x=41时,y2=80,p2=5,则
[5(1+a%)-2(1+50%)]•80(1-40%)×25=3200,
令a%=t,则100t2+15t-2=0,
解得t=
-15±5
| ||
| 200 |
| -15±5×6.40 |
| 200 |
又∵t>0,
∴t≈0.085,
∴a≈8.5.
故a的值为8.5.
点评:此题主要考查了二次函数与一次函数的应用,涉及的知识点有待定系数法求函数解析式,以及根据已知得出利润与销量之间的函数关系式.

练习册系列答案
相关题目
 香蕉味香、富于营养,常食香蕉不仅有益于大脑,预防神经疲劳,还有润肺止咳、防止便秘的作用.今年三月份从3月1日起,“欣欣”香蕉批发店日销售量y1(箱)与时间第x(天)的函数关系如下表:
香蕉味香、富于营养,常食香蕉不仅有益于大脑,预防神经疲劳,还有润肺止咳、防止便秘的作用.今年三月份从3月1日起,“欣欣”香蕉批发店日销售量y1(箱)与时间第x(天)的函数关系如下表:
| 第x(天) | 1 | 2 | 3 | 4 | … |
| 日销售量y1(箱) | 22 | 24 | 26 | 28 | … |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出三月份日销售量y1(元)与时间第x(天)之间的函数关系式;观察右图,直接写出四月份日销售量y2(元)与时间第x(天)之间的一次函数关系式;
(2)请问第几天香蕉日销售利润W最大,最大日销售利润是多少元?
(3)进入五月,由于南海局势持续紧张,中国加强了对菲律宾香蕉进口的审查,市场上来自菲律宾的香蕉锐减,受此影响,与4月10日发生“黄岩岛事件”那天相比,5月10日该店的销售量下降了4a%,每千克售价提高了a%,成本增加了50%,5月10日的销售利润为3200元.请参考以下数据,计算出a的值(结果精确到0.1).
(参考数据:
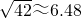 ,
,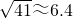 ,
,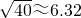 )
)