题目内容
如图，小明站在C处看甲乙两楼楼顶上的点A和点E，C、E、A三点在同一条直线上，点B，D分别在点E，A的正下方，B，C相距20米，D，C相距40米，乙楼高BE为15米，甲楼高AD（ ）米（忽略小明身高）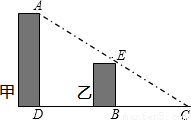
A．40
B．20
C．15
D．30
【答案】分析：由题可知，AD和BC平行，所以有相似三角形，根据对应边成比例列式求解即可．
解答：解：∵AD∥BE
∴△CBE∽△CDA．
∴
，即
．
∴AD=
=30（米）．
故选D
点评：本题考查相似三角形性质的应用．解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．
解答：解：∵AD∥BE
∴△CBE∽△CDA．
∴
，即．∴AD=
=30（米）．故选D
点评：本题考查相似三角形性质的应用．解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．
练习册系列答案
相关题目
15、如图，小明站在C处看甲乙两楼楼顶上的点A和点E．C，E，A三点在同一条直线上，点B，E分别在点E，A的正下方且D，B，C三点在同一条直线上．B，C相距20米，D，C相距40米，乙楼高BE为15米，甲楼高AD为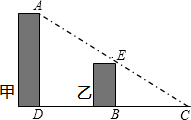
如图，小明站在C处看甲乙两楼楼顶上的点A和点E，C、E、A三点在同一条直线上，点B，D分别在点E，A的正下方，B，C相距20米，D，C相距40米，乙楼高BE为15米，甲楼高AD（ ）米（忽略小明身高）
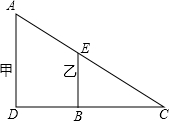如图，小明站在C处看甲、乙两楼楼顶的点A和E，A、E、C三点在同一直线上，甲乙两楼的底部D、B与C也在同一直线上，测得BC相距20米，DB相距20米，乙楼高BE为15米，则甲楼高（小明身高忽略不计）为