题目内容
(2012•茂名)每年六七月份我市荔枝大量上市,今年某水果商以5元/千克的价格购进一批荔枝进行销售,运输过程中质量损耗5%,运输费用是0.7元/千克,假设不计其他费用.
(1)水果商要把荔枝售价至少定为多少才不会亏本?
(2)在销售过程中,水果商发现每天荔枝的销售量m(千克)与销售单价x(元/千克)之间满足关系:m=-10x+120,那么当销售单价定为多少时,每天获得的利润w最大?
(1)水果商要把荔枝售价至少定为多少才不会亏本?
(2)在销售过程中,水果商发现每天荔枝的销售量m(千克)与销售单价x(元/千克)之间满足关系:m=-10x+120,那么当销售单价定为多少时,每天获得的利润w最大?
分析:(1)设购进荔枝k千克,荔枝售价定为y元/千克时,水果商要不亏本,由题意建立不等式求出其值就可以了.
(2)由(1)可知,每千克荔枝的平均成本为6元,再根据售价-进价=利润就可以表示出w,然后化为顶点式就可以求出最值.
(2)由(1)可知,每千克荔枝的平均成本为6元,再根据售价-进价=利润就可以表示出w,然后化为顶点式就可以求出最值.
解答:解:(1)设购进荔枝k千克,荔枝售价定为y元/千克时,水果商才不会亏本,由题意得
y•k(1-5%)≥(5+0.7)k,
∵k>0,
∴95%y≥5.7
∴y≥6
所以,水果商要把荔枝售价至少定为6元/千克才不会亏本.
(2)由(1)可知,每千克荔枝的平均成本为6元,由题意得
w=(x-6)m
=(x-6)(-10x+120)
=-10(x-9)2+90,
∵a=-10<0
∴w有最大值
∴当x=9时,w有最大值.
所以,当销售单价定为9元/千克时,每天可获利润w最大.
y•k(1-5%)≥(5+0.7)k,
∵k>0,
∴95%y≥5.7
∴y≥6
所以,水果商要把荔枝售价至少定为6元/千克才不会亏本.
(2)由(1)可知,每千克荔枝的平均成本为6元,由题意得
w=(x-6)m
=(x-6)(-10x+120)
=-10(x-9)2+90,
∵a=-10<0
∴w有最大值
∴当x=9时,w有最大值.
所以,当销售单价定为9元/千克时,每天可获利润w最大.
点评:本题考查了不等式的运用,二次函数的顶点式在解决实际问题中求最值的运用.在解答中求出荔枝的平均进价是关键.

练习册系列答案
相关题目
 (2012•茂名)一个正方体的表面展开图如图所示,则原正方体的“建”字所在的面的对面所标的字是( )
(2012•茂名)一个正方体的表面展开图如图所示,则原正方体的“建”字所在的面的对面所标的字是( )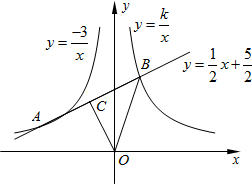 象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.
象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.