Question

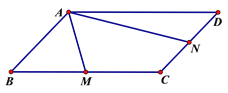
【题目】如图，在平行四边形 中，点 是 边上任意一点，连接 ．过点 作线段 的平行线，交 延长线于点 ．

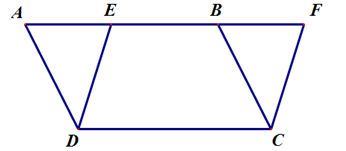
（1）证明： ．
（2）过点 作 ，垂足为点 ．点 为 边中点，连接 ， ．
① 根据题意完成作图；
② 猜想线段 ， 的数量关系，并写出你的证明思路．

Answer 1

【答案】
（1）

证明：∵四边形 是平行四边形

∴ ，

又∵

∴四边形 是平行四边形

∴

∴

∴

∴

（2）

解：①作图：

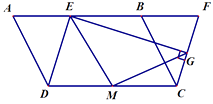
②猜想： ；

证明思路：

延长 ， 交于点

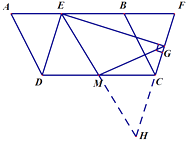
证明

得到

在 中，得到

【解析】（1）由平行四边形的性质得AB=CD ， AB∥CD；由两组对边分别平行得四边形 DEFC 是平行四边形；由平行四边形的性质得EF=CD；
由等量代换得 AE=BF；
（2）①如图；②猜想： M E = M G ；延长 EM ， FC 交于点 H由已知条件证明△DEM≌△CHM，由全等三角形的性质得ME=MH；在 Rt△EHG 中，得到 ME=MG.
【考点精析】利用直角三角形斜边上的中线和平行四边形的判定与性质对题目进行判断即可得到答案，需要熟知直角三角形斜边上的中线等于斜边的一半；若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积．