题目内容
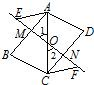 17、如图所示,AD∥BC,AB∥DC,点O为线段AC的中点,过点O作一条直线分别与AB、CD交于点M、N、点E、F在直线MN上,且OE=OF.图中全等的三角形共有
17、如图所示,AD∥BC,AB∥DC,点O为线段AC的中点,过点O作一条直线分别与AB、CD交于点M、N、点E、F在直线MN上,且OE=OF.图中全等的三角形共有4
对.分析:O是中点,AO=CO,∠1=∠2(对顶角相等),AD∥BC所以∠MAC=∠NCA所以△AOM≌△ACN,因为OE=OF,所以△AOE≌△COF,所以△CFN≌△AME,四边形ABCD是平行四边形,所以△ABC≌△ADC,一共四对.
解答:解:∵AD∥BC,AB∥CD
∴四边形ABCD是平行四边形
∴AB=CD,AD=BC,∠B=∠D
∴△ABC≌△ADC
∵O是AC的中点
∴AO=CO,∠1=∠2(对顶角相等)
∵AB∥CD∴∠MAO=∠NOC
∴△MAO≌△NCO
∴OM=ON
∵OE=OF,∠1=∠2,AO=CO
∴ME=FN,△AEO≌△FCO
∴∠E=∠F,AE=CF
∴△AEM≌△CFN
∴一共四对全等三角形.
故填4

∴四边形ABCD是平行四边形
∴AB=CD,AD=BC,∠B=∠D
∴△ABC≌△ADC
∵O是AC的中点
∴AO=CO,∠1=∠2(对顶角相等)
∵AB∥CD∴∠MAO=∠NOC
∴△MAO≌△NCO
∴OM=ON
∵OE=OF,∠1=∠2,AO=CO
∴ME=FN,△AEO≌△FCO
∴∠E=∠F,AE=CF
∴△AEM≌△CFN
∴一共四对全等三角形.
故填4
点评:本题考查的是三角形全等的判定,关键是先找哪两个三角形全等,再根据全等的性质作为下一对三角形全等判定的依据.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=n°,则∠BOC=
如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=n°,则∠BOC= 直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点Q随之停止运动.设运动时间为t(秒).
直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点Q随之停止运动.设运动时间为t(秒). 直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点P随之停止运动.设运动时间为t(秒).
直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点P随之停止运动.设运动时间为t(秒). 如图所示,AD∥BC,DCG是一条直线,∠1=∠2,∠3=∠4.求证:DE∥CF.
如图所示,AD∥BC,DCG是一条直线,∠1=∠2,∠3=∠4.求证:DE∥CF. 如图所示,AD∥BC,∠BAD=∠BCD,那么直线AB与CD平行吗?请说明理由.
如图所示,AD∥BC,∠BAD=∠BCD,那么直线AB与CD平行吗?请说明理由.