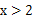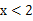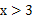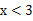题目内容
在平面直角坐标系中,已知点A(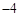 ,0),B(2,0),若点C在一次函数
,0),B(2,0),若点C在一次函数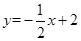 的图象上,且△ABC为直角三角形,则满足条件的点C有 ( )
的图象上,且△ABC为直角三角形,则满足条件的点C有 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
D.
解析试题分析:由题意知,直线y=-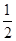 x+2与x轴的交点为(4,0),与y轴的交点为(0,2),如图:
x+2与x轴的交点为(4,0),与y轴的交点为(0,2),如图:
过点A作垂线与直线的交点W(-4,4),
过点B作垂线与直线的交点S(2,1),
过AB中点E(-1,0),作垂线与直线的交点为F(-1,2.5),
则EF=2.5<3,
所以以3为半径,以点E为圆心的圆与直线必有两个交点
∴共有四个点能与点A,点B组成直角三角形.
故选D.
考点:1.勾股定理的逆定理;2.一次函数图象上点的坐标特征;3.圆周角定理.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
甲、乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图所示,则下列说法正确的是( )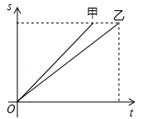
| A.甲、乙两人的速度相同 | B.甲先到达终点 |
| C.乙用的时间短 | D.乙比甲跑的路程多 |
反比例函数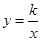 与一次函数
与一次函数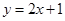 的图像的一个交点是(1,k),则
的图像的一个交点是(1,k),则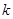 的值为( )
的值为( )
| A.﹣2 | B.2 | C.﹣3 | D.3 |
方程x2+3x-l=0由于x壬0,因此可化为x+3= ,则原方程的根可视为函数y=x+3与y=
,则原方程的根可视为函数y=x+3与y= 图像交点的横坐标,利用图像估计一元三次方程x3+2x2-2=0的根x0所在的范围是
图像交点的横坐标,利用图像估计一元三次方程x3+2x2-2=0的根x0所在的范围是
| A.1<x0<2 | B.0<x0<l | C.-l<x0<0 | D.-2<x0<-l |
若方程 =x+1的解x0满足1<x0<2,则k可能是( )
=x+1的解x0满足1<x0<2,则k可能是( )
| A.1 | B.2 | C.3 | D.6 |
一辆汽车和一辆摩托车分别从 两地去同一城市,它们离
两地去同一城市,它们离 地的路程随时间变化的图像如图所示,则下列结论错误的是( )
地的路程随时间变化的图像如图所示,则下列结论错误的是( ) 
A.摩托车比汽车晚到 |
B. 两地的路程为 两地的路程为 |
C.摩托车的速度为 |
D.汽车的速度为 |
 (千米)与时间
(千米)与时间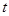 (小时)之间函数关系的大致图象是( )
(小时)之间函数关系的大致图象是( )
 的图象与x、y轴分别交于点A、B,点P
的图象与x、y轴分别交于点A、B,点P 为直线AB上的一动点(
为直线AB上的一动点(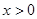 )过P作PC
)过P作PC y轴于点C,若使
y轴于点C,若使 的面积大于
的面积大于 的面积,则P的横坐标x的取值范围是( )
的面积,则P的横坐标x的取值范围是( )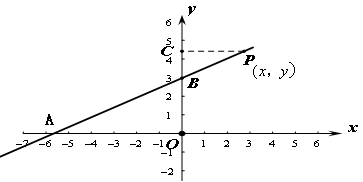
 B、
B、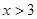 C、
C、 D、
D、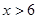
 轴于(2,0),交
轴于(2,0),交 轴于(0,3),当函数值大于0时,
轴于(0,3),当函数值大于0时,