题目内容
【题目】已知:点 A、C、B、D在同一条直线,∠M=∠N,AM=CN.请你添加一个条件,使△ABM≌△CDN,并给出证明.
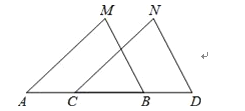
(1)你添加的条件是: ;
(2)证明:
【答案】∠MAB=∠NCD,或BM=DN或∠ABM=∠CDN.
【解析】
试题分析:判定两个三角形全等的一般方法有:ASA、SSS、SAS、AAS、HL,所以可添加条件为∠MAB=∠NCD,或BM=DN或∠ABM=∠CDN.
试题解析:(1)你添加的条件是:①∠MAB=∠NCD;
(2)证明:在△ABM和△CDN中
∵∠M=∠N,AM=CM,∠MAB=∠NCD
∴△ABM≌△CDN(ASA),
故答案为:∠MAB=∠NCD;
在△ABM和△CDN中
∵∠M=∠N,AM=CM,∠MAB=∠NCD
∴△ABM≌△CDN(ASA).

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目