题目内容
如图,一次函数y=-2x+2的图象与与坐标轴相交于A、B两点,点P(x,y)是线段AB(不含端点)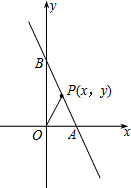 上一动点,设△AOP的面积为S.
上一动点,设△AOP的面积为S.(1)求点B的坐标;
(2)求S关于x的函数关系式,并写出自变量x的取值范围;
(3)当S=
| 1 | 2 |
分析:(1)从图中不难发现,点B在y轴上,即B点的横坐标为0,且点B在一次函数y=-2x+2的图象上,则将x=0代入即可求得y值,B点坐标即可确定.
(2)根据A点为一次函数y=-2x+2的图象与与x轴的交点,不难确定A点的坐标为(1,0).再运用三角形的面积计算公式,即可用求得△AOP的面积为S关于x的解析式.
(3)首先根据(2)可求得P的坐标值.再设B关于x轴的对称点为B′,连接PB′,交x轴于Q,Q点即为所求.B′点的坐标根据B点坐标不难求得.因而利用P、B的坐标求得PB′的解析式,再联立组成方程组求得Q点的坐标值.
(2)根据A点为一次函数y=-2x+2的图象与与x轴的交点,不难确定A点的坐标为(1,0).再运用三角形的面积计算公式,即可用求得△AOP的面积为S关于x的解析式.
(3)首先根据(2)可求得P的坐标值.再设B关于x轴的对称点为B′,连接PB′,交x轴于Q,Q点即为所求.B′点的坐标根据B点坐标不难求得.因而利用P、B的坐标求得PB′的解析式,再联立组成方程组求得Q点的坐标值.
解答: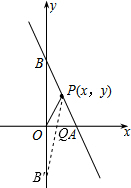 解:(1)当x=0时,y=-2×0+2=2,
解:(1)当x=0时,y=-2×0+2=2,
即B(0,2);
(2)当y=0时,0=-2x+2,
解得x=1,
∴A(1,0),即OA=1,
∴S△AOP=
×OA×yP=
×1×(-2x+2)=-x+1,
即S=-x+1,其中0<x<1;
(3)∵S=
,
∴
=-x+1,
解得x=
,
把x=
代入y=-2x+2,可得y=1,
即P(
,1),
设B关于x轴的对称点为B′,连接PB′,交x轴于Q,Q点即为所求,如图.
∵B′(0,-2),设经过PB′的直线解析式为y=kx+b,于是
,
解得k=6,b=-2,
∴PB′的解析式为y=6x-2,
令y=0时,解得x=
,
即Q(
,0).
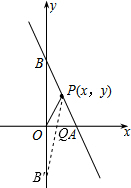 解:(1)当x=0时,y=-2×0+2=2,
解:(1)当x=0时,y=-2×0+2=2,即B(0,2);
(2)当y=0时,0=-2x+2,
解得x=1,
∴A(1,0),即OA=1,
∴S△AOP=
| 1 |
| 2 |
| 1 |
| 2 |
即S=-x+1,其中0<x<1;
(3)∵S=
| 1 |
| 2 |
∴
| 1 |
| 2 |
解得x=
| 1 |
| 2 |
把x=
| 1 |
| 2 |
即P(
| 1 |
| 2 |
设B关于x轴的对称点为B′,连接PB′,交x轴于Q,Q点即为所求,如图.
∵B′(0,-2),设经过PB′的直线解析式为y=kx+b,于是
|
解得k=6,b=-2,
∴PB′的解析式为y=6x-2,
令y=0时,解得x=
| 1 |
| 3 |
即Q(
| 1 |
| 3 |
点评:本题是一次函数与三角形相结合的问题,在图形中渗透运动的观点是中考中经常出现的问题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数