题目内容
【题目】解答题
(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF; 
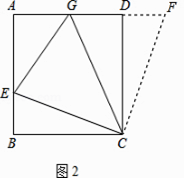
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD. 
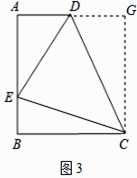
(3)运用(1)(2)解答中所积累的经验和知识,完成下题: 如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠B=∠CDF=90°,
∵∠ADC=90°,
∴∠FDC=90°.
∴∠B=∠FDC,
∵BE=DF,
∴△CBE≌△CDF(SAS).
∴CE=CF.
(2)证明:如图2,延长AD至F,使DF=BE,连接CF.
由(1)知△CBE≌△CDF,
∴∠BCE=∠DCF.
∴∠BCE+∠ECD=∠DCF+∠ECD,
即∠ECF=∠BCD=90°,
又∠GCE=45°,
∴∠GCF=∠GCE=45°.
∵CE=CF,GC=GC,
∴△ECG≌△FCG.
∴GE=GF,
∴GE=GF=DF+GD=BE+GD.
(3)解:如图3,过C作CG⊥AD,交AD延长线于G.
在直角梯形ABCD中,
∵AD∥BC,
∴∠A=∠B=90°,
又∵∠CGA=90°,AB=BC,
∴四边形ABCG为正方形.
∴AG=BC.
∵∠DCE=45°,
根据(1)(2)可知,ED=BE+DG.
∴10=4+DG,
即DG=6.
设AB=x,则AE=x﹣4,AD=x﹣6,
在Rt△AED中,
∵DE2=AD2+AE2,即102=(x﹣6)2+(x﹣4)2.
解这个方程,得:x=12或x=﹣2(舍去).
∴AB=12.
∴S梯形ABCD= ![]() (AD+BC)AB=
(AD+BC)AB= ![]() ×(6+12)×12=108.
×(6+12)×12=108.
即梯形ABCD的面积为108.
【解析】(1)由四边形是ABCD正方形,易证得△CBE≌△CDF(SAS),即可得CE=CF;(2)首先延长AD至F,使DF=BE,连接CF,由(1)知△CBE≌△CDF,易证得∠ECF=∠BCD=90°,又由∠GCE=45°,可得∠GCF=∠GCE=45°,即可证得△ECG≌△FCG,继而可得GE=BE+GD;(3)首先过C作CG⊥AD,交AD延长线于G,易证得四边形ABCG为正方形,由(1)(2)可知,ED=BE+DG,即可求得DG的长,设AB=x,在Rt△AED中,由勾股定理DE2=AD2+AE2 , 可得方程,解方程即可求得AB的长,继而求得直角梯形ABCD的面积.
【考点精析】本题主要考查了勾股定理的概念和正方形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】为了了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.1 |
70≤x<80 | 90 | n |
80≤x<90 | m | 0.4 |
90≤x≤100 | 60 | 0.2 |
请根据以上图表中提供的信息,解答下列问题:
(1)本次调查的样本容量为;
(2)在表中:m= , n=;
(3)补全频数分布直方图;
(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在分数段内;
(5)如果比赛成绩80分以上(含80分)为优秀,那么你估计该竞赛项目的优秀率大约是 .





