题目内容
已知p、q、r均为质数,且pq+qp=r,求p、q、r的值.
考点:质数与合数
专题:计算题
分析:根据质数的定义及pq+qp=r可以得出p、q中必有一个质数为2,再由pq+qp=r进行分析就可以求出p、q和r的值.
解答:解:∵p、q、r均为质数,且pq+qp=r,
∴p、q两个数中,必有一个是偶数,
而质数中只有一个数2是偶数,
∴p=2或q=2,
∴当p=2,q=3时,r=17;
当q=2,p=3时,r=17.
故p=2,q=3,r=17或q=2,p=3,r=17.
∴p、q两个数中,必有一个是偶数,
而质数中只有一个数2是偶数,
∴p=2或q=2,
∴当p=2,q=3时,r=17;
当q=2,p=3时,r=17.
故p=2,q=3,r=17或q=2,p=3,r=17.
点评:本题考查了质数与合数的关系的运用,奇数、偶数的性质的运用,解答时合理利用质数中唯一的偶数2是关键.

练习册系列答案
相关题目
已知Rt△ABC中,∠B=90°,AC=6,⊙O是△ABC外接圆,则⊙O半径等于( )
| A、3 | B、4 | C、5 | D、6 |
不能判断四边形ABCD为平行四边形的题设是( )
| A、AB平行且等于CD |
| B、AB=AD,∠B=∠D |
| C、AB=CD,AD=BC |
| D、∠A=∠C,∠B=∠D |
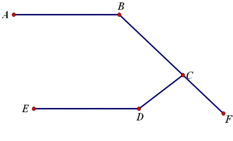 如图,是某交通地图路线,其中AB∥DE,测得∠B=130°,∠DCF=105°,则∠D的度数为( )
如图,是某交通地图路线,其中AB∥DE,测得∠B=130°,∠DCF=105°,则∠D的度数为( )| A、155° | B、125° |
| C、140° | D、135° |
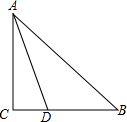 在Rt△ABC中,∠C=90°,∠B=45°,D为BC上一点,且BD=2
在Rt△ABC中,∠C=90°,∠B=45°,D为BC上一点,且BD=2