题目内容
 (1997•四川)已知一次函数y=kx+b的图象与另一个一次函数y=3x+2的图象相交于y轴上的点A,且x轴下方的一点B(3,n)在一次函数y=kx+b的图象上n满足关系式|n|=3-
(1997•四川)已知一次函数y=kx+b的图象与另一个一次函数y=3x+2的图象相交于y轴上的点A,且x轴下方的一点B(3,n)在一次函数y=kx+b的图象上n满足关系式|n|=3-| 4 | n |
(1)求这个一次函数的解析式;
(2)在直角坐标系内画出(1)题中函数的图象(要求列表、描点、连线).
分析:(1)先确定A点坐标为(0,2),由于点B(3,n)在x轴的下方得到n<0,则分式方程为-n=3-
,解得n1=-4,n2=1(舍去),即点B的坐标为(3,-4),然后利用待定系数法确定一次函数的解析式;
(2)取两组对应值,即x=0,y=2;x=1,y=0,然后描点、连线即可得到一次函数的图象.
| 4 |
| n |
(2)取两组对应值,即x=0,y=2;x=1,y=0,然后描点、连线即可得到一次函数的图象.
解答:解:(1)对于y=3x+2,令x=0,则y=2,即直线y=3x+2与y轴的交点为(0,2),
∴点A的坐标为(0,2),
∵点B(3,n)在x轴的下方,
∴n<0.
∴-n=3-
,
解得n1=-4,n2=1(舍去),
∴点B的坐标为(3,-4),
又∵点A(0,2)、B(3,-4)在一次函数y=kx+b的图象上,
∴
,
解得
.
∴这个一次函数的解析式为 y=-2x+2;
(2)列表
描点、连线,如图
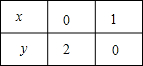
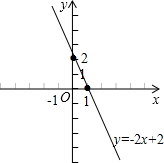 .
.
∴点A的坐标为(0,2),
∵点B(3,n)在x轴的下方,
∴n<0.
∴-n=3-
| 4 |
| n |
解得n1=-4,n2=1(舍去),
∴点B的坐标为(3,-4),
又∵点A(0,2)、B(3,-4)在一次函数y=kx+b的图象上,
∴
|
解得
|
∴这个一次函数的解析式为 y=-2x+2;
(2)列表
描点、连线,如图

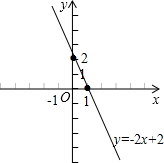 .
.点评:本题考查了两直线平行或相交的问题:直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)平行,则k1=k2;若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相交,则交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目