Question

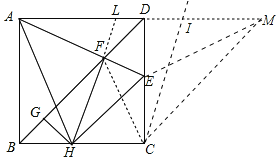
【题目】如图，正方形ABCD 中，AB＝4，E为CD上一动点，连接AE交BD于F，过F作FH⊥AE于F，过H 作HG⊥BD 于 G．则下列结论：①AF＝FH；②∠HAE＝45°；③BD＝2FG；④△CEH 的周长为 8．其中正确的个数是（ ）

A.1个B.2个C.3个D.4个

Answer 1

【答案】D

【解析】

①作辅助线，延长HF交AD于点L，连接CF，通过证明△ADF≌△CDF，可得：AF=CF，故需证明FC=FH，可证：AF=FH；

②由FH⊥AE，AF=FH，可得：∠HAE=45°；

③作辅助线，连接AC交BD于点O，证BD=2FG，只需证OA=GF即可，根据△AOF≌△FGH，可证OA=GF，故可证BD=2FG；

④作辅助线，延长AD至点M，使AD=DM，过点C作CI∥HL，则IL=HC，可证AL=HE，再根据△MEC≌△MIC，可证：CE=IM，故△CEH的周长为边AM的长．

①连接FC，延长HF交AD于点L，

∵BD为正方形ABCD的对角线，

∴∠ADB=∠CDF=45°．

∵AD=CD，DF=DF，

∴△ADF≌△CDF．

∴FC=AF，∠ECF=∠DAF．

∵∠ALH+∠LAF=90°，

∴∠LHC+∠DAF=90°．

∵∠ECF=∠DAF，

∴∠FHC=∠FCH，

∴FH=FC．

∴FH=AF．

②∵FH⊥AE，FH=AF，

∴∠HAE=45°．

③连接AC交BD于点O，可知：BD=2OA，

∵∠AFO+∠GFH=∠GHF+∠GFH，

∴∠AFO=∠GHF．

∵AF=HF，∠AOF=∠FGH=90°，

∴△AOF≌△FGH．

∴OA=GF．

∵BD=2OA，

∴BD=2FG．

④连接EM，延长AD至点M，使AD=DM，过点C作CI∥HL，则：LI=HC，

∵HL⊥AE，CI∥HL，

∴AE⊥CI，

∴∠DIC+∠EAD=90°，

∵∠EAD+∠AED=90°，

∴∠DIC=∠AED，

∵ED⊥AM，AD=DM，

∴EA=EM，

∴∠AED=∠MED，

∴∠DIC=∠DEM，

∴∠CIM=∠CEM，

∵CM=MC，∠ECM=∠CMI=45°，

∴△MEC≌△CIM，可得：CE=IM，

同理，可得：AL=HE，

∴HE+HC+EC=AL+LI+IM=AM=8．

∴△CEH的周长为8，为定值．

故①②③④结论都正确．

故选D．