题目内容
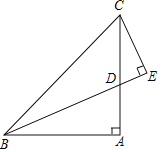
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC时
(1)若CE⊥BD于E,①∠ECD=___________0;②求证:BD=2EC;
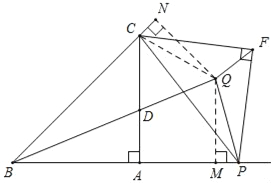
(2)如图,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点.当点P运动时,点Q是否一定在射线BD上?若在,请证明,若不在;请说明理由.
【答案】22.5.
【解析】(1)①先运用三角形内角和定理,得出∠ABD=∠ECD,再根据∠ABD=22.5°,得到∠ECD=22.5°;②延长CE交BA的延长线于点G,通过判定△ABD≌△ACG,得出BD=CG=2CE即可;
(2)连接CQ,过点Q作QM⊥BP于M,作QN⊥BC于N,在等腰直角△CPF中,求得∠QCP=∠QPC=22.5°,进而得出△PQC中,∠PQC=135°;在四边形QNBM中,根据QM⊥BP,QN⊥BC,∠ABC=45°,得到∠MQN=135°,进而得到∠NQC=∠MQP,根据AAS判定△QPM≌△QCN,得出QM=QN,最后根据角平分线的性质定理的逆定理,得出点Q一定在射线BD上.
解:(1)①∵∠BAC=90°,CE⊥BD,∠ADB=∠CDE,
∴∠ABD=∠ECD,
又∵∠BAC=90°,AB=AC,BD平分∠ABC,
∴∠ABD=22.5°,
∴∠ECD=22.5°;
故答案为:22.5.
②如图,延长CE交BA的延长线于点G,

∵BD平分∠ABC,CE⊥BD,
∴CE=GE,
在△ABD与△ACG中,
∠DBA=∠ACG,∠BAC=∠CAG,AB=AC,
∴△ABD≌△ACG(AAS),
∴BD=CG=2CE;
(2)点Q一定在射线BD上,
理由:如图,连接CQ,过点Q作QM⊥BP于M,作QN⊥BC于N,
∵QF为∠PFC的角平分线,△CPF为等腰直角三角形,
∴QF为PC的垂直平分线,
∴PQ=QC,
∵Q为∠FPC与∠PFC的角平分线的交点,
∴CQ平分∠FCP,
∵△CPF为等腰直角三角形,
∴∠FCP=∠FPC=45°,
∴∠QCP=∠QPC=22.5°,
∴△PQC中,∠PQC=135°,
∵在四边形QNBM中,QM⊥BP,QN⊥BC,∠ABC=45°,
∴∠MQN=135°,
∴∠MQN=∠PQC,
∴∠NQC=∠MQP,
又∵QC=QP,QM⊥BP,QN⊥BC,
∴△QPM≌△QCN(AAS),
∴QM=QN,
又∵QM⊥BP,QN⊥BC,
∴点Q一定在射线BD上.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案