题目内容
在平面直角坐标系内有线段AB、CD,其中A(3,1),B(4,3),C(6,2),D(8,6),若CD上有一点P的坐标为(a,b),则直线OP与AB的交点的坐标为
(
a,
b)
| 1 |
| 2 |
| 1 |
| 2 |
(
a,
b)
.| 1 |
| 2 |
| 1 |
| 2 |
分析:建立直角坐标系,找出A、B、C和D的位置,那么连接BD,直线BD一定过原点O,连接AC直线AC一定过原点O,且B是OD的中点,同理A是OC的中点,于是AB是△OCD的中位线,从CD上任取一点P(a、b),则直线OP与AB的交点的坐标为(
a,
b).
| 1 |
| 2 |
| 1 |
| 2 |
解答: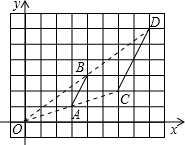 解:建立直角坐标系,找出A、B、C和D的位置如图所示:
解:建立直角坐标系,找出A、B、C和D的位置如图所示:
∵AB∥CD,且O,B,D三点在一条直线上,OB=BD,
∴OP=PE,
∴若点P的坐标为(a,b),
则直线OP与AB的交点的坐标为(
a,
b).
故答案为:(
a,
b).
 解:建立直角坐标系,找出A、B、C和D的位置如图所示:
解:建立直角坐标系,找出A、B、C和D的位置如图所示:∵AB∥CD,且O,B,D三点在一条直线上,OB=BD,
∴OP=PE,
∴若点P的坐标为(a,b),
则直线OP与AB的交点的坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查位似变换的知识,在直角坐标系中找出A、B、C和D的位置是解决本题的前提条件,由AB∥CD联想到三角形相似,或平行线分线段成比例定理,是解决这道题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 在平面直角坐标系内有两点A(-2,0),B(
在平面直角坐标系内有两点A(-2,0),B(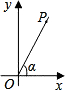 如图,在平面直角坐标系内有一点P(5,12),那么OP与x轴正半轴的夹角α的余弦值
如图,在平面直角坐标系内有一点P(5,12),那么OP与x轴正半轴的夹角α的余弦值