题目内容
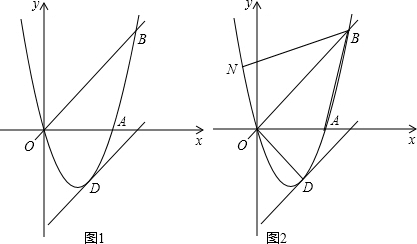
 (2013•昭通)如图,在⊙C的内接△AOB中,AB=AO=4,tan∠AOB=
(2013•昭通)如图,在⊙C的内接△AOB中,AB=AO=4,tan∠AOB=| 3 | 4 |
(1)求抛物线的解析式;
(2)直线m与⊙C相切于点A,交y轴于点D,动点P在线段OB上,从点O出发向点B运动,同时动点Q在线段DA上,从点D出发向点A运动,点P的速度为每秒1个单位长,点Q的速度为每秒2个单位长.当PQ⊥AD时,求运动时间t的值.
分析:(1)利用待定系数法求二次函数解析式解析式即可;
(2)连接AC交OB于E,作OF⊥AD于F,得出m∥OB,进而求出OD,OF的长,进而利用勾股定理得出DF的长.
(2)连接AC交OB于E,作OF⊥AD于F,得出m∥OB,进而求出OD,OF的长,进而利用勾股定理得出DF的长.
解答: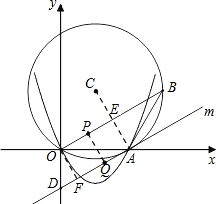 解:(1)将点A(4,0)和点(-2,6)的坐标代入y=a(x-2)2+m中,得方程组,
解:(1)将点A(4,0)和点(-2,6)的坐标代入y=a(x-2)2+m中,得方程组,
解得
,
故抛物线的解析式为y=
x2-2x.
(2)如图所示,连接AC交OB于E.作OF⊥AD于F,
∵直线m切⊙C于点A,
∴AC⊥m.
∵弦AB=AO,
∴
=
.
∴AC⊥OB,
∴m∥OB.
∴∠OAD=∠AOB.
∵OA=4,tan∠AOB=
,
∴OD=OA•tan∠OAD=4×
=3.
则OF=OA•sin∠OAD=4×
=2.4.
t秒时,OP=t,DQ=2t,
若PQ⊥AD,则 FQ=OP=t.DF=DQ-FQ=t.
∴△ODF中,t=DF=
=1.8(秒).
 解:(1)将点A(4,0)和点(-2,6)的坐标代入y=a(x-2)2+m中,得方程组,
解:(1)将点A(4,0)和点(-2,6)的坐标代入y=a(x-2)2+m中,得方程组,
|
解得
|
故抛物线的解析式为y=
| 1 |
| 2 |
(2)如图所示,连接AC交OB于E.作OF⊥AD于F,
∵直线m切⊙C于点A,
∴AC⊥m.
∵弦AB=AO,
∴
 |
| OA |
 |
| AB |
∴AC⊥OB,
∴m∥OB.
∴∠OAD=∠AOB.
∵OA=4,tan∠AOB=
| 3 |
| 4 |
∴OD=OA•tan∠OAD=4×
| 3 |
| 4 |
则OF=OA•sin∠OAD=4×
| 3 |
| 5 |
t秒时,OP=t,DQ=2t,
若PQ⊥AD,则 FQ=OP=t.DF=DQ-FQ=t.
∴△ODF中,t=DF=
| OD2-OF2 |
点评:此题主要考查了二次函数的综合应用以及垂径定理的推论和勾股定理等知识,根据切线的性质以及锐角三角函数关系得出OF的长是解题关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
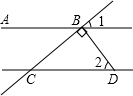 (2013•昭通)如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是( )
(2013•昭通)如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是( )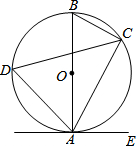 (2013•昭通)如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠B=60°.
(2013•昭通)如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠B=60°. (2013•昭通)如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(2013•昭通)如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.