题目内容
In the Rt△ABC,∠ACB=90°,AB+BC+CA=2+| 6 |
分析:根据告诉的斜边的中线的长为1,求得斜边的长,则两直角边的和等于
,然后设出一直角边的长,利用勾股定理得到方程,将两直角边求出来,计算它们的积即可.
| 6 |
解答:解:∵斜边的中线的长为1,
∴斜边AB的长为2,
∴BC+CA=2+
-AB=2+
-2=
,
设BC的长为x,则AC的长为
-x,
根据勾股定理得:x2+(
-x)2=22
整理得:x2-
x+1=0
∵BC+CA=
,
∴AC•BC=1,
故答案为1.
∴斜边AB的长为2,
∴BC+CA=2+
| 6 |
| 6 |
| 6 |
设BC的长为x,则AC的长为
| 6 |
根据勾股定理得:x2+(
| 6 |
整理得:x2-
| 6 |
∵BC+CA=
| 6 |
∴AC•BC=1,
故答案为1.
点评:本题考查了勾股定理的相关知识,同时题目中还应用到了一元二次方程根与系数的关系,是一道不错的综合考题.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 16、In Fig.,In the Rt△ABC,∠ACB=90°,∠A=30°,CD is the bisector to∠ACB,MD is the perpendicular to BA and MD through the midpoint of segment AB,then∠CDM=
16、In Fig.,In the Rt△ABC,∠ACB=90°,∠A=30°,CD is the bisector to∠ACB,MD is the perpendicular to BA and MD through the midpoint of segment AB,then∠CDM=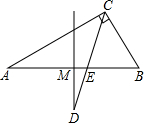 In Fig,In the Rt△ABC,∠ACB=90°,∠A=30°,CD is the bisector to∠ACB,MD is the perpendicular to BA and MD through the midpoint of segment AB,then∠CDM=________.
In Fig,In the Rt△ABC,∠ACB=90°,∠A=30°,CD is the bisector to∠ACB,MD is the perpendicular to BA and MD through the midpoint of segment AB,then∠CDM=________.