题目内容
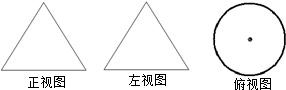
如图所示，是一个几何体的三视图，已知正视图和左视图都是边长为2的等边三角形，则这个几何体的全面积为
- A.2л
- B.3л
- C.
л - D.（1+）л
B
分析：易得此几何体为圆锥，那么全面积为：底面积+侧面积=π×底面半径2+π×底面半径×母线长．
解答：此几何体为圆锥，底面直径为2，母线长为2，那么底面半径为1，
∴圆锥的全面积=π×12+π×1×2=3π，故选B．
点评：主要考查了圆锥的全面积的公式；解决本题的关键是得到圆锥的底面直径与母线长．
分析：易得此几何体为圆锥，那么全面积为：底面积+侧面积=π×底面半径2+π×底面半径×母线长．
解答：此几何体为圆锥，底面直径为2，母线长为2，那么底面半径为1，
∴圆锥的全面积=π×12+π×1×2=3π，故选B．
点评：主要考查了圆锥的全面积的公式；解决本题的关键是得到圆锥的底面直径与母线长．
练习册系列答案
相关题目
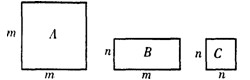28、三种不同类型的矩形地砖长宽如图所示，若现有A类4块，B类4块，C类2块，要拼成一个正方形，则应多余出1块
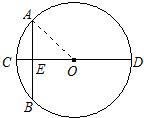17、“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题，“今有圆材，埋壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”用现在的数学语言表述是：“如图所示，CD为⊙O的直径，CD⊥AB，垂足为E，CE=1寸，AB=1尺，求直径CD长是多少寸？”（注：1尺=10寸）
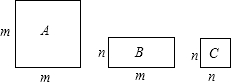三种不同类型的长方形地砖长度如图所示，若有A型4块，B型4块，C型2块，要拼成一个正方形，则应多余出1块