题目内容
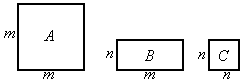
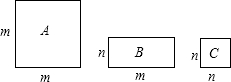
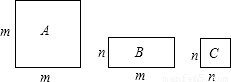
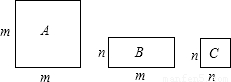
 28、三种不同类型的矩形地砖长宽如图所示,若现有A类4块,B类4块,C类2块,要拼成一个正方形,则应多余出1块
28、三种不同类型的矩形地砖长宽如图所示,若现有A类4块,B类4块,C类2块,要拼成一个正方形,则应多余出1块C
型地砖;这样的地砖拼法表示了一个两数和的平方的几何意义,这个两数和的平方是(2m+n)2=4m2+4mn+n2
.分析:分别计算出4块A的面积和4块B的面积、2块C的面积,再计算这三种类型的砖的总面积,用完全平方公式化简后,即可得出多了哪种类型的地砖.
解答:解:4块A的面积为:4×m×m=4m2;
4块B的面积为:4×m×n=4mn;
2块C的面积为2×n×n=2n2;
那么这三种类型的砖的总面积应该是:
4m2+4mn+2n2=4m2+4mn+n2+n2=(2m+n)2+n2,
因此,多出了一块C型地砖,拼成的正方形的面积为(2m+n)2=4m2+4mn+n2.
故答案为:C;(2m+n)2=4m2+4mn+n2.
4块B的面积为:4×m×n=4mn;
2块C的面积为2×n×n=2n2;
那么这三种类型的砖的总面积应该是:
4m2+4mn+2n2=4m2+4mn+n2+n2=(2m+n)2+n2,
因此,多出了一块C型地砖,拼成的正方形的面积为(2m+n)2=4m2+4mn+n2.
故答案为:C;(2m+n)2=4m2+4mn+n2.
点评:本题考查了完全平方公式的几何意义,立意较新颖,注意面积的不同求解是解题的关键,对此类问题的要深入理解.

练习册系列答案
相关题目