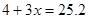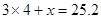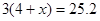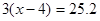题目内容
乘积为-240的不同五个整数的平均值最大是 。
A.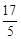 | B.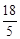 | C.7 | D.9 。 |
D
显然是要使得负因数的绝对值尽量小,且正因数尽量大,符合的负因数只能为-1,然后正因数为1,2,3,40,再根据平均数的求法求出五个整数的平均值.
解:∵要求乘积为-240的不同五个整数的最大平均值,
又∵-1×1×2×3×40=-240,
∴平均值最大的五个因数为-1,1,2,3,40,
∴五个整数的平均值为(-1+1+2+3+40)÷5=9.
故选D.
解:∵要求乘积为-240的不同五个整数的最大平均值,
又∵-1×1×2×3×40=-240,
∴平均值最大的五个因数为-1,1,2,3,40,
∴五个整数的平均值为(-1+1+2+3+40)÷5=9.
故选D.

练习册系列答案
相关题目
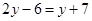 变形为
变形为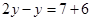 ,这种变形叫___________,根据是____________.
,这种变形叫___________,根据是____________.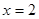 时,
时,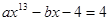 ,则当
,则当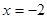 时,
时,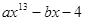 =_____。
=_____。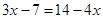
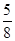 与六年级人数的
与六年级人数的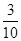 都是120人,那么两个年级的人数比较( )
都是120人,那么两个年级的人数比较( )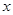 千米/时,列方程得( )
千米/时,列方程得( )