题目内容
a＞0，b＜0且a+b＜0，用“＜”连接a，b，-a，-b，a-b，b-a为
b-a＜b＜-a＜a＜-b＜a-b
b-a＜b＜-a＜a＜-b＜a-b
．分析：由于a＞0，b＜0且a+b＜0，可得到|b|＞a，a-b＞0，b-a＜0，则-b＞a，b＜-a，a-b＞-b，b-a＜b，
解答：解：∵a＞0，b＜0且a+b＜0，
∴|b|＞a，a-b＞0，b-a＜0，
∴-b＞a，b＜-a，a-b＞-b，b-a＜b，
∴a，b，-a，-b，a-b，b-a的大小关系为b-a＜b＜-a＜a＜-b＜a-b．
故答案为b-a＜b＜-a＜a＜-b＜a-b．
∴|b|＞a，a-b＞0，b-a＜0，
∴-b＞a，b＜-a，a-b＞-b，b-a＜b，
∴a，b，-a，-b，a-b，b-a的大小关系为b-a＜b＜-a＜a＜-b＜a-b．
故答案为b-a＜b＜-a＜a＜-b＜a-b．
点评：本题考查了有理数的大小比较：正数大于零，负数小于零；负数的绝对值越大，这个数反而越小．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
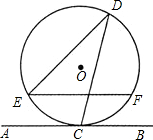如图，直线AB与半径为2的⊙O相切于点C，D是⊙O上一点，且∠EDC=30°，弦EF∥AB，则EF的长度为（ ）| A、2 | ||
B、2
| ||
C、
| ||
D、2
|
若代数式
有意义，则x的取值范围是（ ）
| ||
|
| A、x≤3 |
| B、x≥1 |
| C、1≤x≤3 |
| D、1≤x≤3且x≠2 |
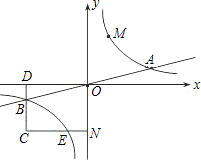A点左侧）是双曲线y=