题目内容
(12分)如图1,在平面上,给定了半径为![]() 的⊙
的⊙![]() ,对于任意点
,对于任意点![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,使得
,使得![]() ·
·![]() =
=![]() ,这种把点
,这种把点![]() 变为点
变为点![]() 的变换叫做反演变换,点
的变换叫做反演变换,点![]() 与点
与点![]() 叫做互为反演点,⊙
叫做互为反演点,⊙![]() 称为基圆.
称为基圆.
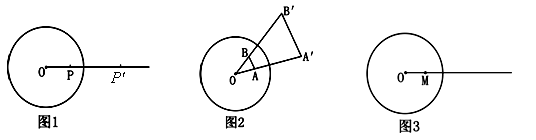
⑴如图2,⊙![]() 内有不同的两点
内有不同的两点![]() 、
、![]() ,它们的反演点分别是
,它们的反演点分别是![]() 、
、![]() ,则与∠
,则与∠![]() 一定相等的角是( ▲ )
一定相等的角是( ▲ )
(A)∠![]() (B)∠
(B)∠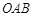 (C)∠
(C)∠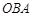 (D)∠
(D)∠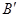
⑵如图3,⊙![]() 内有一点
内有一点![]() ,请用尺规作图画出点
,请用尺规作图画出点![]() 的反演点
的反演点![]() ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).
⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆![]() 的半径为
的半径为![]() ,另一个半径为
,另一个半径为![]() 的⊙
的⊙![]() ,作射线
,作射线![]() 交⊙
交⊙![]() 于点
于点![]() 、
、![]() ,点
,点![]() 、
、![]() 关于⊙
关于⊙![]() 的反演点分别是
的反演点分别是![]() 、
、![]() ,点
,点![]() 为⊙
为⊙![]() 上另一点,关于⊙
上另一点,关于⊙![]() 的反演点为
的反演点为![]() .求证:∠
.求证:∠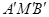 =90°.
=90°.

(1)(C)
(2)过![]() 作
作![]() ⊥
⊥![]() 交⊙
交⊙![]() 于点
于点![]() ,连
,连![]() .
.
过![]() 作
作![]() ⊥
⊥![]() 交射线
交射线![]() 于点
于点![]() .
.
点![]() 即为所求.
即为所求.
(3)连![]() 、
、![]() .
.
∵![]() 是⊙
是⊙![]() 直径,
直径,
∴∠![]() =90°.
=90°.
∵∠![]() 是△
是△![]() 的外角,
的外角,
∴∠![]() -∠
-∠![]() =∠
=∠![]() .
.
∵点![]() 、
、![]() 关于⊙
关于⊙![]() 的反演点分别是
的反演点分别是![]() ,
,![]() .
.
∴![]()
∴△![]() △
△![]()
∴∠![]() ∠
∠![]()
同理:△![]() △
△![]()
∴∠![]() ∠
∠![]()
由等式性质知:
∠![]() -∠
-∠![]() =∠
=∠![]() -∠
-∠![]()
∴∠![]() =∠
=∠![]()
即∠![]() =90°
=90°
解析:此题主要考查的是相似三角形的判定与性质;点与圆的位置关系

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
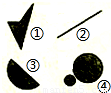
 下面是小马虎解的一道题:
下面是小马虎解的一道题: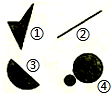 由平面上的点组成图形A,如果连接A中任意两点的线段必定在A内,则称A为平面上的凸图形.给出如图所示的平面上的4个图形(阴影区域及其边界),其中为凸图形的是
由平面上的点组成图形A,如果连接A中任意两点的线段必定在A内,则称A为平面上的凸图形.给出如图所示的平面上的4个图形(阴影区域及其边界),其中为凸图形的是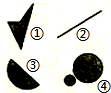 由平面上的点组成图形A,如果连接A中任意两点的线段必定在A内,则称A为平面上的凸图形.给出如图所示的平面上的4个图形(阴影区域及其边界),其中为凸图形的是________(写出所有凸图形的序号)
由平面上的点组成图形A,如果连接A中任意两点的线段必定在A内,则称A为平面上的凸图形.给出如图所示的平面上的4个图形(阴影区域及其边界),其中为凸图形的是________(写出所有凸图形的序号)