Question

如图，游客从某旅游景区的景点A处下山至C处有两种路径，一中是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C．现有甲、乙两位游客同时从A处下山，甲沿AC匀速步行，速度为45m/min．乙开始从A乘缆车到B，在B处停留5min后，再从B匀速步行到C，两人同时到达．已知缆车匀速直线运动的速度为180m/min，山路AC长为2430m，经测量，∠CAB=45°，∠CBA=105°．（参考数据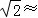：1.4，1.7）

（1）求索道AB的长；

（2）为乙的步行速度．

 

 

Answer 1

(1)AB=1260m；(2)乙的步行速度是45m/min.

【解析】

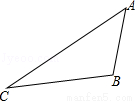
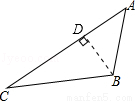
试题分析：（1）如图，过B点作BD垂直于AC，垂足为D点．通过解Rt△BDC得到CD=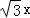，则由CD+AD=AC求得x=900，所以AB=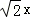=900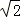=1260m；

（2）分别求得甲沿AC匀速步行到C所用时间、乙从A乘缆车到B所用时间，则易求乙从B匀速步行到C所用的时间为，故乙的步行速度为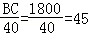m/min．

试题解析：（1）过B点作BD垂直于AC，垂足为D点，

设BD=xm，则AD=xm，

在Rt△BDC中，tan∠BCA=，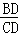

即tan30°=，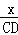

∴CD=，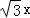

∵CD+AD=AC，

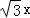∴+x=2430，

解得x=900，

所以AB=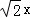=900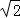=1260m．

（2）甲沿AC匀速步行到C所用时间为，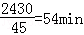

乙从A乘缆车到B所用时间为，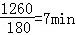

∴乙从B匀速步行到C所用的时间为54﹣2﹣7﹣5=40min，

∴乙的步行速度为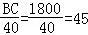m/min．

考点：解直角三角形的应用．