题目内容
（2013•顺义区一模）如图，已知抛物线y=ax2+bx+3与y轴交于点A，且经过B（1，0），C（5，8）两点，点D是抛物线顶点，E是对称轴与直线AC的交点，F与E关于点D对称．（1）求抛物线的解析式；
（2）求证：∠AFE=∠CFE；
（3）在抛物线的对称轴上是否存在点P，使△AFP与△FDC相似？若有，请求出所有符合条件的点P的坐标；若没有，请说明理由．
分析：（1）已知抛物线过B、C两点，而且两点的坐标都已得出，可用待定系数法来求函数的解析式；
（2）由（1）可得抛物线顶点D（2，-1），直线AC的解析式为y=x+3，由E是对称轴与直线AC的交点，可得E点坐标，由F与E关于点D对称，可得F点坐标，从点A、C分别向对称轴作垂线AM、CN，交对称轴于M、N，通过证明Rt△FAM∽Rt△FCN，根据相似三角形的性质即可求解；
（3）在△FDC中，三内角不等，且∠CDF为钝角，分两种情况：①若点P在点F下方时，②若点P在点F上方时，讨论即可求解．
（2）由（1）可得抛物线顶点D（2，-1），直线AC的解析式为y=x+3，由E是对称轴与直线AC的交点，可得E点坐标，由F与E关于点D对称，可得F点坐标，从点A、C分别向对称轴作垂线AM、CN，交对称轴于M、N，通过证明Rt△FAM∽Rt△FCN，根据相似三角形的性质即可求解；
（3）在△FDC中，三内角不等，且∠CDF为钝角，分两种情况：①若点P在点F下方时，②若点P在点F上方时，讨论即可求解．
解答：解：（1）将点B（1，0），C（5，8）代入y=ax2+bx+3得
，
解得
，
所以抛物线的解析式为y=x2-4x+3；
（2）由（1）可得抛物线顶点D（2，-1），
直线AC的解析式为y=x+3，
由E是对称轴与直线AC的交点，则E（2，5），
由F与E关于点D对称，则F（2，-7），
证法一：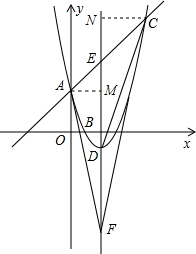
从点A、C分别向对称轴作垂线AM、CN，交对称轴于M、N，
在Rt△FAM和Rt△FCN中
∠AMF=∠CNF=90°，
=
=
=
=
所以Rt△FAM∽Rt△FCN，
所以∠AFE=∠CFE；
证法二：直线AF的解析式为y=-5x+3，
点C（5，8）关于对称轴的对称点是Q（-1，8），
将点Q（-1，8）代入y=-5x+3，可知点Q在直线AF上，
所以∠AFE=∠CFE；
（3）在△FDC中，三内角不等，且∠CDF为钝角
①若点P在点F下方时，
在△AFP中，∠AFP为钝角
因为∠AFE=∠CFE，∠AFE+∠AFP=180°，∠CFE+∠CDF＜180°，
所以∠AFP和∠CDF不相等
所以，点P在点F下方时，两三角形不能相似
②若点P在点F上方时，
由∠AFE=∠CFE，要使△AFP与△FDC相似
只需
=
（点P在DF之间）或
=
（点P在FD的延长线上）
解得点P的坐标为（2，-3）或（2，19）．
|
解得
|
所以抛物线的解析式为y=x2-4x+3；
（2）由（1）可得抛物线顶点D（2，-1），
直线AC的解析式为y=x+3，
由E是对称轴与直线AC的交点，则E（2，5），
由F与E关于点D对称，则F（2，-7），
证法一：
从点A、C分别向对称轴作垂线AM、CN，交对称轴于M、N，在Rt△FAM和Rt△FCN中
∠AMF=∠CNF=90°，
| AM |
| MF |
| 2 |
| 10 |
| 1 |
| 5 |
| 3 |
| 15 |
| CN |
| NF |
所以Rt△FAM∽Rt△FCN，
所以∠AFE=∠CFE；
证法二：直线AF的解析式为y=-5x+3，
点C（5，8）关于对称轴的对称点是Q（-1，8），
将点Q（-1，8）代入y=-5x+3，可知点Q在直线AF上，
所以∠AFE=∠CFE；
（3）在△FDC中，三内角不等，且∠CDF为钝角
①若点P在点F下方时，
在△AFP中，∠AFP为钝角
因为∠AFE=∠CFE，∠AFE+∠AFP=180°，∠CFE+∠CDF＜180°，
所以∠AFP和∠CDF不相等
所以，点P在点F下方时，两三角形不能相似
②若点P在点F上方时，
由∠AFE=∠CFE，要使△AFP与△FDC相似
只需
| AF |
| CF |
| PF |
| DF |
| AF |
| DF |
| PF |
| CF |
解得点P的坐标为（2，-3）或（2，19）．
点评：主要考查待定系数法、方程、函数及三角形相似等知识，考查综合运用数学知识、分析问题、解决问题的能力，考查数形结合、分类讨论的思想．此题是一道以函数为背景的综合压轴题，第1、2两个小题较为容易，上手很轻松，第3小题中很容易看出要讨论相似三角形的对应顶角，想提醒大家的是在中考中应该对可能的情况进行逐一讨论，才能尽量防止漏解．
练习册系列答案
相关题目